Question

已知：如圖，在△ABC中，AB=AC，AD⊥BC，垂足為點D，AN是△ABC外角∠CAM的平分線，CE⊥AN，垂足為點E，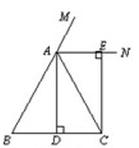

（1）求證：四邊形ADCE為矩形；
（2）當△ABC滿足什么條件時，四邊形ADCE是一個正方形？并給出證明.

Answer 1

（1）先根據等腰三角形的性質證得∠BAD=∠DAC，再根據角平分線的性質可得∠MAE=∠CAE，即可求得∠DAN=90°，再結合AD⊥BC，CE⊥AN即可證得結論；（2）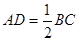

解析試題分析：（1）先根據等腰三角形的性質證得∠BAD=∠DAC，再根據角平分線的性質可得∠MAE=∠CAE，即可求得∠DAN=90°，再結合AD⊥BC，CE⊥AN即可證得結論；
（2）先根據等腰三角形的性質證得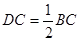，再補充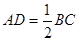可得，DC=AD，由（1）四邊形ADCE為矩形，即可證得矩形ADCE為正方形.
（1）∵在△ABC中，AB=AC，AD⊥BC
∴∠BAD=∠DAC 
∵AN是△ABC外角∠CAM的平分線
∴∠MAE=∠CAE
∴∠DAN=∠DAC+∠CAE=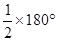=90°
又∵AD⊥BC，CE⊥AN
∴∠ADC=∠CEA=90°
∴四邊形ADCE為矩形；
（2）例如：當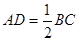時，四邊形ADCE是正方形
∵AB=AC，AD⊥BC于D
∴
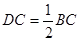
又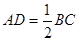
∴DC=AD
由（1）四邊形ADCE為矩形
∴矩形ADCE為正方形.
考點：特殊四邊形的判定
點評：特殊四邊形的判定和性質是初中數學的重點，貫穿于整個初中數學的學習，是中考中比較常見的知識點，一般難度不大，需熟練掌握.