
【題目】如圖,拋物線y=ax2+4x+c與x軸交于A、B兩點,交y軸交于點C,直線y=-x+5經過點B、C.
(1)求拋物線的表達式;
(2)點D(1,0),點P為對稱軸上一動點,連接BP、CP.
①若∠CPB=90°,求點P的坐標;
②點Q為拋物線上一動點,若以C、D、P、Q為頂點的四邊形是平行四邊形,求P的坐標.
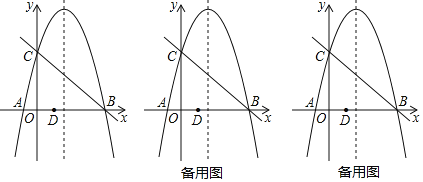
【答案】(1)y=-x2+4x+5;(2)①點P的坐標為(2,-1)或(2,6)②點P的坐標為(2,3),(2,5)或(2,13).
【解析】
(1)利用一次函數圖象上點的坐標特征可求出點B,C的坐標,由點B,C的坐標利用待定系數法即可求出拋物線的表達式;
(2)①利用二次函數的性質可求出拋物線對稱軸為直線x=2,設點P的坐標為(2,m),結合點B,C的坐標可得出BC2,CP2,BP2的值,由∠CPB=90°利用勾股定理可得出關于m的一元二次方程,解之即可得出點P的坐標;
②設點P的坐標為(2,n),分CD為邊及CD為對角線兩種情況考慮:(i)若CD為邊,當四邊形CDPQ(CDQP)為平行四邊形時,由點C,D,P的坐標結合平行四邊形的對角線互相平分可得出點Q的坐標,再利用二次函數圖象上點的坐標特征可求出n的值,進而可得出點P的坐標;(ii)若CD為對角線,四邊形CPDQ為平行四邊形,由點C,D,P的坐標結合平行四邊形的對角線互相平分可得出點Q的坐標,再利用二次函數圖象上點的坐標特征可求出n的值,進而可得出點P的坐標.綜上,此題得解.
解:(1)當x=0時,y=-x+5=5,
∴點C的坐標為(0,5);
當y=0時,-x+5=0,
解得:x=5,
∴點B的坐標為(5,0).
將B(5,0),C(0,5)代入y=ax2+4x+c,得:
![]() ,解得:
,解得:![]() ,
,
∴拋物線的表達式為y=-x2+4x+5.
(2)①∵拋物線的表達式為y=-x2+4x+5,
∴拋物線的對稱軸為直線x=-![]() =2,
=2,
∴設點P的坐標為(2,m).
∵點B的坐標為(5,0),點C的坐標為(0,5),
∴CP2=(2-0)2+(m-5)2=m2-10m+29,BP2=(2-5)2+(m-0)2=m2+9,BC2=(0-5)2+(5-0)2=50.
∵∠CPB=90°,
∴BC2=CP2+BP2,即50=m2-10m+29+m2+9,
解得:m1=-1,m2=6,
∴點P的坐標為(2,-1)或(2,6).
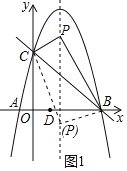
②設點P的坐標為(2,n),分兩種情況考慮(如圖2):
(i)若CD為邊,當四邊形CDPQ為平行四邊形時,
∵點C的坐標為(0,5),點D的坐標為(1,0),點P的坐標為(2,n),
∴點Q的坐標為(0+2-1,5+n-0),即(1,5+n).
∵點Q在拋物線y=-x2+4x+5上,
∴5+n=-1+4+5,解得:n=3,
∴點P的坐標為(2,3);
當四邊形CDQP為平行四邊形時,
∵點C的坐標為(0,5),點D的坐標為(1,0),點P的坐標為(2,n),
∴點Q的坐標為(1+2-0,0+n-5),即(3,n-5).
∵點Q在拋物線y=-x2+4x+5上,
∴n-5=-9+12+5,解得:n=13,
∴點P的坐標為(2,13);
(ii)若CD為對角線,∵四邊形CPDQ為平行四邊形,點C的坐標為(0,5),點D的坐標為(1,0),點P的坐標為(2,n),
∴點Q的坐標為(0+1-2,5+0-n),即(-1,5-n).
∵點Q在拋物線y=-x2+4x+5上,
∴5-n=-1-4+5,解得:n=5,
∴點P的坐標為(2,5).
綜上所述:點P的坐標為(2,3),(2,5)或(2,13).


科目:初中數學 來源: 題型:
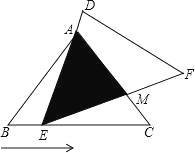
【題目】如圖,在△ABC中,已知AB=AC=5,BC=6,且△ABC≌△DEF,將△DEF與△ABC重合在一起,△ABC不動,△DEF運動,并滿足:點E在邊BC上沿B到C的方向運動,且DE始終經過點A,EF與AC交于M點.
(1)求證:△ABE∽△ECM;
(2)探究:在△DEF運動過程中,重疊部分能否構成等腰三角形?若能,求出BE的長;若不能,請說明理由;
(3)當線段BE為何值時,線段AM最短,最短是多少?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在矩形ABCD中,AB=6cm,BC=12cm,點P從點A出發沿AB以1cm/s的速度向點B移動;同時,點Q從點B出發沿BC以2cm/s的速度向點C移動.設運動時間為t秒.
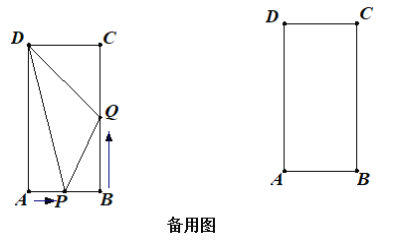
(1)當t=2時,△DPQ的面積為 cm2;
(2)在運動過程中△DPQ的面積能否為26cm2?如果能,求出t的值,若不能,請說明理由;
(3)運動過程中,當 A、P、Q、D四點恰好在同一個圓上時,求t的值;
(4)運動過程中,當以Q為圓心,QP為半徑的圓,與矩形ABCD的邊共有4個交點時,直接寫出t的取值范圍.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】許多家庭以燃氣作為燒水做飯的燃料,節約用氣是我們日常生活中非常現實的問題.某款燃氣灶旋鈕位置從0度到90度,燃氣關閉時,燃氣灶旋鈕位置為0度,旋鈕角度越大,燃氣流量越大,燃氣開到最大時,旋鈕角度為90度.為測試燃氣灶旋鈕在不同位置上的燃氣用量,在相同條件下,選擇在燃氣灶旋鈕的5個不同位置上分別燒開一壺水(當旋鈕角度太小時,其火力不能夠將水燒開,故選擇旋鈕角度![]() 度的范圍是
度的范圍是![]() ),記錄相關數據得到下表:
),記錄相關數據得到下表:
旋鈕角度(度) | 20 | 50 | 70 | 80 | 90 |
所用燃氣量(升) | 73 | 67 | 83 | 97 | 115 |
(1)請你從所學習過的一次函數、反比例函數和二次函數中確定哪種函數能表示所用燃氣量![]() 升與旋轉角度
升與旋轉角度![]() 度的變化規律?說明確定這種函數而不是其他函數的理由,并求出它的解析式;
度的變化規律?說明確定這種函數而不是其他函數的理由,并求出它的解析式;
(2)當旋轉角度為多少時,燒開一壺水所用燃氣量最少?最少是多少?
(3)某家庭使用此款燃氣灶,以前習慣把燃氣開到最大,現采用最節省燃氣的旋轉角度,若該家庭現在每月的平均燃氣用量為13立方米,求現在每月平均能比以前每月節省燃氣多少立方米?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某中學開展了“手機伴我健康行”主題活動。他們隨即抽取部分學生進行“使用手機的目的”和“每周使用手機的時間”的問卷調查,并繪制成如圖①,②的統計圖,已知“查資料”的人數是40人。
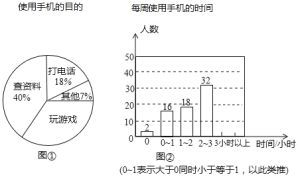
請你根據以上信息解答下列問題:
(1) 在扇形統計圖中,“玩游戲”對應的百分比為___,圓心角度數是___度;
(2)補全條形統計圖;
(3)該校共有學生2100人,估計每周使用手機時間在2小時以上(不含2小時)的人數
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知拋德物線y=![]() +1有下性質:該拋物線上任意一點到定點F(0,2)的距離與到軸的距離始終相等,如圖,點M的坐標為(
+1有下性質:該拋物線上任意一點到定點F(0,2)的距離與到軸的距離始終相等,如圖,點M的坐標為(![]() ,3),P是拋物線y=
,3),P是拋物線y=![]() +1上一個動點,則△PMF周長的最小值是_____.
+1上一個動點,則△PMF周長的最小值是_____.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】二次函數y=a(x﹣h)2+k(a≠0)的圖象是拋物線,定義一種變換,先作這條拋物線關于原點對稱的拋物線y′,再將得到的對稱拋物線y′向上平移m(m>0)個單位,得到新的拋物線ym,我們稱ym叫做二次函數y=a(x﹣h)2+k(a≠0)的m階變換.
(1)已知:二次函數y=2(x+2)2+1,它的頂點關于原點的對稱點為 ,這個拋物線的2階變換的表達式為 .
(2)若二次函數M的6階變換的關系式為y6′=(x﹣1)2+5.
①二次函數M的函數表達式為 .
②若二次函數M的頂點為點A,與x軸相交的兩個交點中左側交點為點B,在拋物線y6′=(x﹣1)2+5上是否存在點P,使點P與直線AB的距離最短,若存在,求出此時點P的坐標.
(3)拋物線y=﹣3x2﹣6x+1的頂點為點A,與y軸交于點B,該拋物線的m階變換的頂點為點C.若△ABC是以AB為腰的等腰三角形,請直按寫出m的值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com