
【題目】已知在![]() 和
和![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() 交
交![]() 于點
于點![]() ,
,![]() 為線段
為線段![]() 上一動點,以每秒
上一動點,以每秒![]() 的速度從
的速度從![]() 勻速運動到
勻速運動到![]() ,過
,過![]() 作直線
作直線![]() ,且
,且![]() ,點
,點![]() 在直線
在直線![]() 的右側,設點
的右側,設點![]() 運動時間為
運動時間為![]() .
.
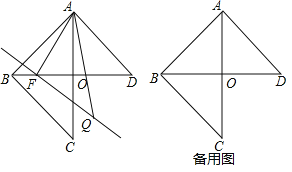
(1)當![]() 為等腰三角形時,
為等腰三角形時,![]() ;
;
(2)當![]() 點在線段
點在線段![]() 上時,過
上時,過![]() 點作
點作![]() 于點
于點![]() ,求證
,求證![]() ;
;
(3)當![]() 點在線段
點在線段![]() 上運動的過程中,
上運動的過程中,![]() 的面積是否變化?若不變,求出它的值.
的面積是否變化?若不變,求出它的值.
【答案】(1)3或6或![]() ;(2)見解析;(3)不變,S△ABQ=9.
;(2)見解析;(3)不變,S△ABQ=9.
【解析】
(1)分三種情況討論,由等腰三角形的性質可求BF的長,即可求t的值;
(2)由等腰三角形的性質可得∠AOB=90°,由“AAS”可證△AOF≌△FHQ;
(3)由“AAS”可證△AOF≌△FHQ,可得OF=QH=t-3,由面積的和差關系可求解.
(1)∵∠BAD=90°,AB=AD,
∴∠ABD=∠ADB=45°,
若AB=AF時,即點F與點D重合,
∴BF=BD=6cm,
∴t=![]() =6,
=6,
若BF=AF時,
∴∠ABF=∠BAF=45°,
∴∠AFB=90°,
∴AF⊥BD,且AB=AD
∴BF=DF=3cm,
∴t=![]() =3,
=3,
若AB=BF=![]() cm,
cm,
∴t=![]() =
=![]()
故答案為:3或6或![]() .
.
(2)如圖1,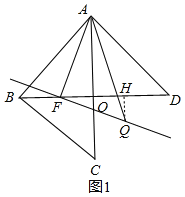
∵∠DAB=∠ABC=90°,AD=AB=CB,
∴∠ABD=∠ADB=45°,∠BAC=∠ACB=45°,
∴∠AOB=90°,
∵AF⊥FQ,QH⊥BD,
∴∠AFQ=∠FHQ=90°,
∴∠QFH+∠FQH=90°,∠AFO+∠QFH=90°,
∴∠AFO=∠FQH,AF=FQ,∠AOF=∠FHQ=90°
∴△AOF≌△FHQ(AAS)
(3)不變,
理由如下:如圖2,過點Q作QH⊥BD,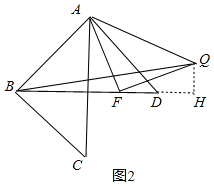
∵∠DAB=∠ABC=90°,AD=AB=CB,
∴∠ABD=∠ADB=45°,∠BAC=∠ACB=45°,
∴∠AOB=90°,
∵AF⊥FQ,QH⊥BD,
∴∠AFQ=∠FHQ=90°,
∴∠QFH+∠FQH=90°,∠AFO+∠QFH=90°,
∴∠AFO=∠FQH,AF=FQ,∠AOF=∠FHQ=90°
∴△AOF≌△FHQ(AAS)
∴OF=QH=t-3,
∵S△ABQ=S△ABF+S△AFQ-S△BFQ=![]() BF×AO+
BF×AO+![]() ×AF2-
×AF2-![]() ×BF×QH
×BF×QH
∴S△ABQ=![]() ×t×3+
×t×3+![]() [32+(t-3)2]-
[32+(t-3)2]-![]() ×t×(t-3)=9
×t×(t-3)=9
故△ABQ的面積不發生變化.


 口算題卡北京婦女兒童出版社系列答案
口算題卡北京婦女兒童出版社系列答案科目:初中數學 來源: 題型:
【題目】如圖,拋物線![]() 經過點
經過點![]() ,與
,與![]() 軸負半軸交于點
軸負半軸交于點![]() ,與
,與![]() 軸交于點
軸交于點![]() ,且
,且![]() .
.
(1)求拋物線的解析式;
(2)點![]() 在
在![]() 軸上,且
軸上,且![]() ,求點
,求點![]() 的坐標;
的坐標;
(3)點![]() 在拋物線上,點
在拋物線上,點![]() 在拋物線的對稱軸上,是否存在以點
在拋物線的對稱軸上,是否存在以點![]() ,
,![]() ,
,![]() ,
,![]() 為頂點的四邊形是平行四邊形?若存在。求出所有符合條件的點
為頂點的四邊形是平行四邊形?若存在。求出所有符合條件的點![]() 的坐標;若不存在,請說明理由.
的坐標;若不存在,請說明理由.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某社區決定購置一批共享單車,經市場調查得知,購買3輛男式單車與4輛女式單車費用相同,購買5輛男式單車與4輛女式單車共需1600元.
(1)求男式單車和女式單車每輛分別是多少元?
(2)該社區要求男式單車比女式單車多4輛,兩種單車至少需要22輛,購置兩種單車的費用不超過5000元,問該社區有幾種購置方案?怎樣的購置才能使所需總費用最低?最低費用是多少?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某校計劃購買一批籃球和足球,已知購買2個籃球和1個足球共需320元,購買3個籃球和2個足球共需540元.
(1)求每個籃球和每個足球的售價;
(2)如果學校計劃購買這兩種球共50個,總費用不超過5500元,那么最多可購買多少個足球?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,四邊形ABCD為平行四邊形,延長AD到E,使DE=AD,連接EB,EC,DB.添加一個條件,不能使四邊形DBCE成為矩形的是( )

(A)AB=BE (B)BE⊥DC (C)∠ADB=90° (D)CE⊥DE
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知![]() 為
為![]() 的高線,
的高線,![]() ,以
,以![]() 為底邊作等腰
為底邊作等腰![]() ,連接
,連接![]() ,
,![]() ,延長
,延長![]() 交
交![]() 于
于![]() 點,下列結論:①
點,下列結論:①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() 為等腰三角形;⑤
為等腰三角形;⑤![]() ,其中正確的有( )
,其中正確的有( )
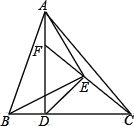
A.①③B.①②④C.①③④D.①②③⑤
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】對于拋物線![]() .
.
![]() 它與
它與![]() 軸交點的坐標為________,與
軸交點的坐標為________,與![]() 軸交點的坐標為________,頂點坐標為________.
軸交點的坐標為________,頂點坐標為________.
![]() 在所給的平面直角坐標系中畫出此時拋物線;
在所給的平面直角坐標系中畫出此時拋物線;
![]() 結合圖象回答問題:當
結合圖象回答問題:當![]() 時,
時,![]() 的取值范圍是________.
的取值范圍是________.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在△ABC中,AD是BC邊上的高線,CE是AB邊上的中線,DG⊥CE于G, CD=AE.
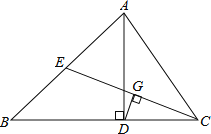
(1)求證: CG=EG.
(2)已知BC=13, CD=5,連結ED,求△EDC 的面積.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com