
【題目】如圖,四邊形OBCD中的三個頂點在⊙O上,點A是優弧BD上的一個動點(不與點B、D重合).

(1)當圓心O在∠BAD內部,∠ABO+∠ADO=60°時,∠BOD= ;
(2)當圓心O在∠BAD內部,四邊形OBCD為平行四邊形時,求∠A的度數;
(3)當圓心O在∠BAD外部,四邊形OBCD為平行四邊形時,請直接寫出∠ABO與∠ADO的數量關系.
【答案】(1)120 °;(2)60°;(3)60°.
【解析】試題分析:(1)連接OA,如圖1,根據等腰三角形的性質得∠OAB=∠ABO,∠OAD=∠ADO,則∠OAB+∠OAD=∠ABO+∠ADO=60°,然后根據圓周角定理易得∠BOD=2∠BAD=120°;(2)根據平行四邊形的性質得∠BOD=∠BCD,再根據圓周角定理得∠BOD=2∠A,則∠BCD=2∠A,然后根據圓內接四邊形的性質由∠BCD+∠A=180°,易計算出∠A的度數;(3)討論:當∠OAB比∠ODA小時,如圖2,與(1)一樣∠OAB=∠ABO,∠OAD=∠ADO,則∠OAD﹣∠OAB=∠ADO﹣∠ABO=∠BAD,由(2)得∠BAD=60°,
所以∠ADO﹣∠ABO=60°;當∠OAB比∠ODA大時,用樣方法得到∠ABO﹣∠ADO=60°.
試題解析:(1)連接OA,如圖1,
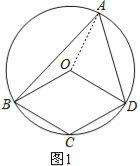
∵OA=OB,OA=OD, ∵∠OAB=∠ABO,∠OAD=∠ADO, ∴∠OAB+∠OAD=∠ABO+∠ADO=60°,即∠BAD=60°,
∴∠BOD=2∠BAD=120°;
(2)∵四邊形OBCD為平行四邊形, ∴∠BOD=∠BCD, ∵∠BOD=2∠A, ∴∠BCD=2∠A,
∵∠BCD+∠A=180°,即3∠A=180°, ∴∠A=60°;
(3)當∠OAB比∠ODA小時,如圖2,

∵OA=OB,OA=OD, ∵∠OAB=∠ABO,∠OAD=∠ADO, ∴∠OAD﹣∠OAB=∠ADO﹣∠ABO=∠BAD,
由(2)得∠BAD=60°, ∴∠ADO﹣∠ABO=60°; 當∠OAB比∠ODA大時,
同理可得∠ABO﹣∠ADO=60°, 綜上所述,|∠ABO﹣∠ADO|=60°.


 智慧課堂密卷100分單元過關檢測系列答案
智慧課堂密卷100分單元過關檢測系列答案 單元期中期末卷系列答案
單元期中期末卷系列答案科目:初中數學 來源: 題型:
【題目】2016年里約奧運會,中國女排的姑娘們在郎平教練指導下,通過刻苦訓練,取得了世界冠軍,為國爭光,如圖,已知排球場的長度OD為18米,位于球場中線處球網的高度AB為2.43米,一隊員站在點O處發球,排球從點O的正上方1.8米的C點向正前方飛出,當排球運行至離點O的水平距離OE為7米時,到達最高點G建立如圖所示的平面直角坐標系.
(1)當球上升的最大高度為3.2米時,求排球飛行的高度y(單位:米)與水平距離x(單位:米)的函數關系式.(不要求寫自變量x的取值范圍).
(2)在(1)的條件下,對方距球網0.5米的點F處有一隊員,他起跳后的最大高度為3.1米,問這次她是否可以攔網成功?請通過計算說明.
(3)若隊員發球既要過球網,又不出邊界,問排球飛行的最大高度h的取值范圍是多少?(排球壓線屬于沒出界)

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】先閱讀,再因式分解:x4+4=(x4+4x2+4)-4x2=(x2+2)2-(2x)2=(x2-2x+2)(x2+2x+2),按照這種方法把多項式x4+64因式分解.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,AB、CD為⊙O的直徑,弦AE∥CD,連接BE交CD于點 F,過點E作直線EP與CD的延長線交于點P,使∠PED=∠C.
(1)求證:PE是⊙O的切線;
(2)求證:ED平分∠BEP;
(3)若⊙O的半徑為5,CF=2EF,求PD的長.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某中學為了解學生平均每天“誦讀經典”的時間,在全校范圍內隨機抽查了部分學生進行調查統計(設每天的誦讀時間為![]() 分鐘),將調查統計的結果分為四個等級:Ⅰ級
分鐘),將調查統計的結果分為四個等級:Ⅰ級![]() 、Ⅱ級
、Ⅱ級![]() 、Ⅲ級
、Ⅲ級![]() 、Ⅳ級
、Ⅳ級![]() .將收集的數據繪制成如下兩幅不完整的統計圖.請根據圖中提供的信息,解答下列問題:
.將收集的數據繪制成如下兩幅不完整的統計圖.請根據圖中提供的信息,解答下列問題:
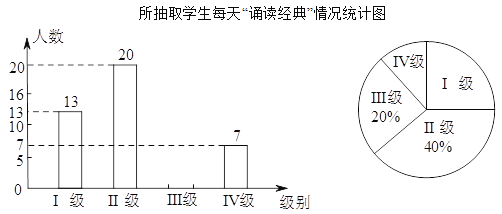
(![]() )請補全上面的條形圖.
)請補全上面的條形圖.
(![]() )所抽查學生“誦讀經典”時間的中位數落在__________級.
)所抽查學生“誦讀經典”時間的中位數落在__________級.
(![]() )如果該校共有
)如果該校共有![]() 名學生,請你估計該校平均每天“誦讀經典”的時間不低于
名學生,請你估計該校平均每天“誦讀經典”的時間不低于![]() 分鐘的學生約有多少人?
分鐘的學生約有多少人?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】數學課上,老師讓學生尺規作圖畫Rt△ABC,使其斜邊AB=c,一條直角邊BC=a.小明的作法如圖所示,你認為這種作法中判斷∠ACB是直角的依據是( )

A. 勾股定理 B. 直徑所對的圓周角是直角
C. 勾股定理的逆定理 D. 90°的圓周角所對的弦是直徑
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com