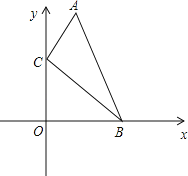
【題目】如圖，點A（a，b）是雙曲線y=
（x＞0）上的一點，點P是x軸負半軸上的一動點，AC⊥y軸于點C，過點A作AD⊥x軸于點D，連接AP交y軸于點B．
（1）△PAC的面積是 ；
（2）當a=2，點P的坐標為（﹣2，0）時，求△ACB的面積．
【答案】（1）4；（2）2．
【解析】
試題分析：（1）由點A（a，b）是雙曲線y=
（x＞0）上，得到ab=8，根據反比例函數系數k的幾何意義，就看得到△PAC的面積=
ADAC=ab=4；
（2）先求出直線AP的解析式為y=x+2，得到B（0，2），即可求出S△ABC=ACBC=×2×2=2．
解：（1）∵點A（a，b）是雙曲線y=（x＞0）上，
∴ab=8，
∵AC⊥y軸于C點，AD⊥x軸于D點，
∴AC=a，AD=b，
∴△PAC的面積=ADAC=ab=4；
故答案為：4；
（2）∵a=2，
∴b=4，
∴AC=2，AD=4，A（2，4），
設直線AP的解析式為y=kx+b，
∴
，
∴
，
∴直線AP的解析式為y=x+2，
∴B（0，2），
∴S△ABC=
ACBC=×2×2=2．
科目：初中數學 來源： 題型：
【題目】如圖，在平行四邊形ABCD中，過點A作AE⊥BC，垂足為E，連接DE，F為線段DE上一點，且∠AFE=∠B.
（1）求證：△ADF∽△DEC；
（2）若AB=8，AD=6
，AF=4，求AE的長．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖所示，三架飛機P，Q，R保持編隊飛行，某時刻在坐標系中的坐標分別為（－1，1），（－3，1），（－1，－1），30秒后，飛機P飛到P′（4，3）位置，則飛機Q，R的位置Q′，R′分別為（ ）
A. Q′（2，3），R′（4，1） B. Q′（2，3），R′（2，1）
C. Q′（2，2），R′（4，1） D. Q′（3，3），R′（3，1）
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，在直角坐標系中，點A、B的坐標分別為（1，4）和（3，0），點C是y軸上的一個動點，且A、B、C三點不在同一條直線上，當△ABC的周長最小時，點C的坐標是（ ）
A．（0，0） B．（0，1） C．（0，2） D．（0，3）
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】小明為了解本班全體同學在閱讀方面的情況，采取全面調查的方法，從喜歡閱讀“科普常識、小說、漫畫、營養美食”等四類圖書中調查了全班學生的閱讀情況(要求每位學生只能選擇一種自己喜歡閱讀的圖書類型)根據調查的結果繪制了下面兩幅不完整的統計圖，如圖所示：
請你根據圖中提供的信息解答下列問題：
（1）該班的學生人數為________人，并把條形統計圖補充完整；
（2）在扇形統計圖中，表示“漫畫”類所對圓心角是________度，喜歡閱讀“營養美食”類圖書的人數占全班人數的百分比為_______；
（3）如果喜歡閱讀“營養美食”類圖書的4 名學生中有3名男生和1名女生，現在打算從中隨機選出2名學生參加學校組織的“營養美食”知識大賽，請用列表或畫樹狀圖的方法，求選出的2名學生中恰好有1名男生和1名女生的概率。
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】下列說法正確的有（ ）
①最大的負整數是﹣1；
②數軸上表示﹣3和3的點到原點的距離相等；
③1.32×104是精確到百分位；
④a+6一定比a大；
⑤（﹣2）4與﹣24結果相等．
A. 2個 B. 3個 C. 4個 D. 0個
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】設
， 
，……， 
，（n為正整數）
（1）試說明
是8的倍數；
（2）若△ABC的三條邊長分別為
、
、
（
為正整數）
①求
的取值范圍.
②是否存在這樣的
，使得△ABC的周長為一個完全平方數，若存在，試舉出一例，若不存在，說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com