【題目】在平面直角坐標系
中，點
.點P第1次向右平移1個單位長度，向下平移2個單位長度至點
，接著，第2次向右平移1個單位長度，向上平移3個單位長度至點
，第3次向右平移1個單位長度，向下平移4個單位長度至點
，第4次向右平移1個單位長度，向上平移5個單位至點
，…，按照此規律，點
第2019次平移至點
的坐標是
A.
B.
C.
D.
開心蛙口算題卡系列答案科目：初中數學 來源： 題型：
【題目】下列說法中正確的是（ ）
A.有且只有一條直線與已知直線垂直；
B.從直線外一點到這條直線的垂線段，叫做這點到這條直線距離；
C.互相垂直的兩條線段一定相交；
D.直線
外一點
與直線上各點連接而成的所有線段中，最短線段的長度是
，則點到直線的距離是.
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，在平行四邊形ABCD中，對角線相交于點O，AC=AB， E是AB邊的中點，G、F為 BC上的點，連接OG和EF，若AB=13， BC=10，GF=5，則圖中陰影部分的面積為( )
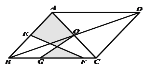
A.48B.36C.30D.24
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，某校數學興趣小組利用自制的直角三角形硬紙板DEF來測量操場旗桿AB的高度，他們通過調整測量位置，使斜邊DF與地面保持平行，并使邊DE與旗桿頂點A在同一直線上，已知DE＝0.5米，EF＝0.25米，目測點D到地面的距離DG＝1.5米，到旗桿的水平距離DC＝20米，求旗桿的高度．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如下圖，
和
是等腰直接角三角形，
，點
為
邊上一點，連接
，
交于點
，點恰好是中點，連接
.
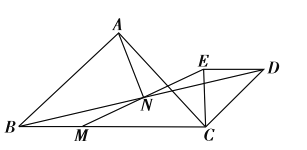
（1）求證：
；
（2）連接AM、AE，請探究AN與EN的位置關系與數量關系。
①寫出AN與EM:位置關系___；數量關系___；
②請證明上述結論.
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖所示，在第1個
中，
；在邊
上任取一點
，延長
到
，使
，得到第2個
；在邊
上任取一點
，延長
到
，使
，得到第3個
…按此做法繼續下去，則第
個三角形中以
為頂點的底角度數是（ ）
A.
B.
C.
D.
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】在平面直角坐標系中，
為坐標原點，將三角形
進行平移，平移后點
的對應點分別是點
，點
，點
，點
，點
.
（1）若
，求
的值；
（2）若點
，其中
. 直線
交
軸于點
，且三角形
的面積為1，試探究
和
的數量關系，并說明理由.
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖所示，菱形
的頂點
在
軸上，點
在點
的左側，點
在
軸的正半軸上.點
的坐標為
.動點
從點出發，以每秒1個單位長度的速度，按照
的順序在菱形的邊上勻速運動一周，設運動時間為
秒.
(1)①點的坐標 .②求菱形的面積.
(2)當
時，問線段
上是否存在點
，使得
最小，如果存在，求出 最小值;如果不存在，請說明理由.
(3)若點到的距離是1，則點運動的時間等于 .
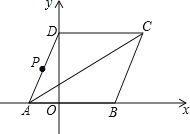
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】“格子乘法”是15世紀中葉，意大利數學家帕喬利在《算術幾何及比例性質摘要》一書中介紹的一種兩個數的相乘的計算方法．這種方法傳入中國之后，在明朝數學家程大位的《算法統宗》書中被稱為“鋪地錦”具體步驟如下：
①先畫一個矩形，把它分成p×q個方格（p，q分別為兩乘數的位數）在方格上邊、右邊分別寫下兩個因數；
②再用對角線把方格一分為二，分別記錄上述各位數字相應乘積的十位數與個位數；
③然后這些乘積由右下到左上，沿對角線方向相加，相加滿十時向前進一；
④最后得到結果（方格左側與下方數字依次排列）．比如：
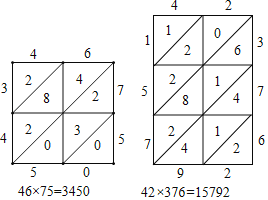
（1）圖1是用“鋪地錦”計算x9×784的格子，則z＝ ，x9×784＝
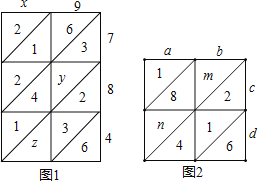
（2）圖2是用“鋪地錦”計算ab×cd的格子，已知ab×cd＝2176，求m和n的值．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
