
【題目】國家推行“節能減排,低碳經濟”政策后,低排量的汽車比較暢銷,某汽車經銷商購進A、B兩種型號的低排量汽車,其中A型汽車的進貨單價比B型汽車的進貨單價多2萬元;花50萬元購進A型汽車的數量與花40萬元購進B型汽車的數量相同.
(1)求A、B兩種型號汽車的進貨單價;
(2)銷售中發現A型汽車的每周銷量yA(臺)與售價x(萬元/臺)滿足函數關系yA=﹣x+20,B型汽車的每周銷量yB(臺)與售價x(萬元/臺)滿足函數關系yB=﹣x+14,A型汽車的售價比B型汽車的售價高2萬元/臺.問A、B兩種型號的汽車售價各為多少時,每周銷售這兩種汽車的總利潤最大?最大利潤是多少萬元?
【答案】(1)A、B兩種型號汽車的進貨單價為:10萬元、8萬元;(2)A、B兩種型號的汽車售價各為14萬元、12萬元時,每周銷售這兩種汽車的總利潤最大,最大利潤是32萬元..
【解析】
(1)由題意根據購進兩種型號的汽車數量相同列出分式方程即可求解;
(2)由題意根據銷售利潤等于每臺汽車的利潤乘以銷售量列出二次函數關系即可求解.
解:(1)設B型汽車的進貨單價為x萬元,根據題意得![]() =
=![]() ,解得x=8,
,解得x=8,
經檢驗x=8是原分式方程的根.
答:A、B兩種型號汽車的進貨單價為:10萬元、8萬元.
(2)設兩種汽車的總利潤為w萬元,根據題意得
w=(x+2﹣10)[﹣(x+2)+18]+(x﹣8)(﹣x+14)
=﹣2x2+48x﹣256
=﹣2(x﹣12)2+32
∵﹣2<0,當x=12時,w有最大值為32.
答:A、B兩種型號的汽車售價各為14萬元、12萬元時,每周銷售這兩種汽車的總利潤最大,最大利潤是32萬元.


科目:初中數學 來源: 題型:
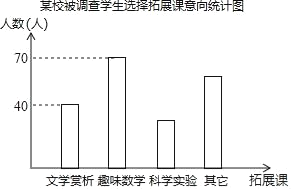
【題目】為豐富學生的課余生活,某校記劃開展三種拓展課活動,分別是“文學賞析”,“趣味數學”,“科學實驗”等項目,要求每位學生自主選擇其中一項拓展課參加.隨機抽取該校各年段部分學生,對選擇拓展課的意向進行調査,將調查的結果制作成以下統計圖和不完整的統計表.
某校被調查學生選擇拓展課意向統計表
選擇意向 | 所占百分比 |
文學賞析 |
|
趣味數學 | 35% |
科學實驗 |
|
其它 | 30% |
(1)該校有2000名學生,請你估計大約有多少名學生參加科學實驗拓展課,并補全統計表.
(2)該校參加科學實驗拓展課的學生隨機分成A,B,C三個人數相同的班級.小慧和小明都參加科學實驗拓展課,求他們同班級的概率(畫樹狀圖或列表法求解)
查看答案和解析>>
科目:初中數學 來源: 題型:
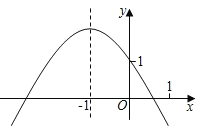
【題目】已知二次函數y=ax2+bx+c的圖象如圖所示,有以下結論:
①a+b+c<0;②a﹣b+c>1;③abc>0;④9a﹣3b+c<0;⑤c﹣a>1.其中所有正確結論的序號是( )
A.①②B.①③④C.①②③④D.①②③④⑤
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】我們知道,三角形的三條角平分線交于一點,這個點稱為三角形的內心(即三角形內切圓的圓心) . 現在規定,如果四邊形的四條角平分線交于一點,我們把這個點稱為“四邊形的內心”.
問題提出
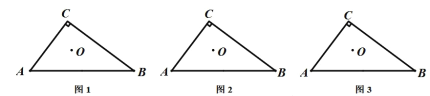
(1)如圖1,在△ABC中,∠C=90°,點O為△ABC的內心,若直線DE分別交邊AC、BC于點D、E,且點O仍然為四邊形ABED的內心,這樣的直線DE可以畫多少條?請在圖1中畫出一條符合條件的直線DE,并簡要說明畫法.
問題探究
(2)如圖2,在△ABC中,∠C=90°, AC=3, BC=4,若滿足(1)中條件的一條直線DE // AB,求此時線段DE的長;
問題解決
(3)如圖3,在△ABC中,∠C=90°, AC=3,BC=4,問滿足(1)中條件的線段DE是否存在最小值?如果存在,請求出這個值;如果不存在,請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
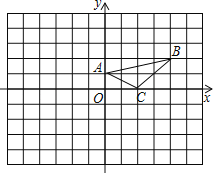
【題目】如圖,在平面直角坐標系中,A(0,1),B(4,2),C(2,0).
(1)將△ABC沿y軸翻折得到△A1B1C1,畫出△A1B1C1;
(2)將△ABC繞著點(﹣1,﹣1)旋轉180°得到△A2B2C2,畫出△A2B2C2;
(3)線段B2C2可以看成是線段B1C1繞著平面直角坐標系中某一點逆時針旋轉得到,直接寫出旋轉中心的坐標為 .
查看答案和解析>>
科目:初中數學 來源: 題型:
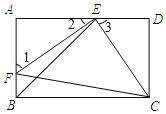
【題目】如圖,E,F分別是矩形ABCD的邊AD,AB上的點,若EF=EC,且EF⊥EC.
(1)求證:△AEF≌△DCE;
(2)若CD=1,求BE的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】觀察下列等式:
(1)第1個等式:a1=![]() ; 第2個等式:a2=
; 第2個等式:a2=![]() ;
;
第3個等式:a3=![]() ; 第4個等式:a4=
; 第4個等式:a4=![]() ;
;
…
用含有n的代數式表示第n個等式:an=___________=___________(n為正整數);
(2)按一定規律排列的一列數依次為![]() ,1,
,1, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,…,按此規律,這列數中的第100個數是_______________.
,…,按此規律,這列數中的第100個數是_______________.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】揚州某風景區門票價格如圖所示,有甲、乙兩個旅行團隊,計劃在端午節期間到該景點游玩,兩團隊游客人數之和為100人,若乙團隊人數不超過40人,甲團隊人數不超過80人,設甲團隊人數為![]() 人,如果甲、乙兩團隊分別購買門票,兩團隊門票款之和為
人,如果甲、乙兩團隊分別購買門票,兩團隊門票款之和為![]() 元.
元.

(1)直接寫出![]() 關于
關于![]() 的函數關系式,并寫出自變量
的函數關系式,并寫出自變量![]() 的取值范圍;
的取值范圍;
(2)計算甲、乙兩團隊聯合購票比分別購票最多可節約多少錢?
(3)該景區每年11月、12月為淡季,景區決定在這兩個月實行門票打五折的優惠(打折期間不售團體票),以吸引大量游客,提高景區收入;景區經過調研發現,隨著接待游客數的增加,景區的運營成本也隨之增加,景區運營成本![]() (萬元)與兩個月游客總人數
(萬元)與兩個月游客總人數![]() (萬人)之間滿足函數關系式:
(萬人)之間滿足函數關系式:![]() ;兩個月游客總人數
;兩個月游客總人數![]() (萬人)滿足:
(萬人)滿足:![]() ,且淡季每天游客數基本相同;為了獲得最大利潤,景區決定通過網絡預約購票的方式控制淡季每天游客數,請問景區的決定是否正確?并說明理由.(利潤
,且淡季每天游客數基本相同;為了獲得最大利潤,景區決定通過網絡預約購票的方式控制淡季每天游客數,請問景區的決定是否正確?并說明理由.(利潤![]() 門票收入
門票收入![]() 景區運營成本)
景區運營成本)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在以O為原點的直角坐標系中,點A,C分別在x軸、y軸的正半軸上,點B在第一象限內,四邊形OABC是矩形,反比例函數y=![]() (x>0)與AB相交于點D,與BC相交于點E,若BE=4CE,四邊形ODBE的面積是8,則k=_____.
(x>0)與AB相交于點D,與BC相交于點E,若BE=4CE,四邊形ODBE的面積是8,則k=_____.

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com