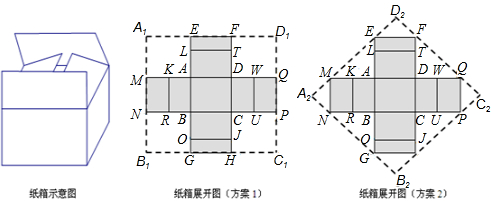
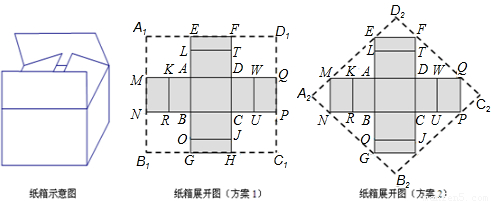
解:(1)①∵紙箱的高為0.5米,底面是黃金矩形(寬與長的比是黃金比,取黃金比為0.6),體積為0.3立方米,
∴假設底面長為x,寬就為0.6x,
∴體積為:0.6x•x•0.5=0.3,
解得:x=1,
∴AD=1,CD=0.6,
DW=KA=DT=JC=0.5,FT=JH=

CD=0.3,
WQ=MK=

AD=

,
∴QM=

+0.5+1+0.5+

=3,
FH=0.3+0.5+0.6+0.5+0.3=2.2,
∴矩形硬紙板A
1B
1C
1D
1的面積是3×2.2=6.6平方米;
②從節省材料的角度考慮,采用方案2(如圖)的菱形硬紙板A
2B
2C
2D
2做一個紙箱比方案1更優,
∵如圖可知△MAE,△NBG,△HCF,△FDQ面積相等,且和為2個矩形FDQD
1,
又∵菱形的性質得出,對角線分別等于矩形的長與寬的菱形的面積小于矩形的面積;
∴從節省材料的角度考慮,采用方案2(如圖)的菱形硬紙板A
2B
2C
2D
2做一個紙箱比方案1更優,
(2)∵將紙箱的底面周長、底面面積和高都設計為原來的一半時,
∴邊長為:0.5,0.3,底面積將變為:0.3×0.5=0.15,
將變為原來的

,高再變為原來的一半時,體積將變為原來的

,
∴水果商的要求不能辦到.
分析:(1)①利用寬與長的比是黃金比,取黃金比為0.6,假設底面長為x,寬就為0.6x,再利用圖形得出QM=

+0.5+1+0.5+

=3,FH=0.3+0.5+0.6+0.5+0.3=2.2,進而求出即可;
②根據菱形的性質得出,對角線乘積的一半絕對小于矩形邊長乘積即可得出答案;
(2)根據相似三角形的性質面積比等于相似比的平方得出即可.
點評:此題主要考查了一元二次方程的應用以及正方形性質與菱形性質等知識,根據題意得出DW=KA=DT=JC=0.5,FT=JH=12CD=0.3,WQ=MK=12AD=12是解決問題的關鍵.

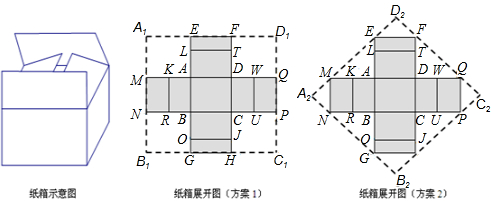
 CD=0.3,
CD=0.3, AD=
AD= ,
, +0.5+1+0.5+
+0.5+1+0.5+ =3,
=3, ,高再變為原來的一半時,體積將變為原來的
,高再變為原來的一半時,體積將變為原來的 ,
, +0.5+1+0.5+
+0.5+1+0.5+ =3,FH=0.3+0.5+0.6+0.5+0.3=2.2,進而求出即可;
=3,FH=0.3+0.5+0.6+0.5+0.3=2.2,進而求出即可;

 新活力總動員暑系列答案
新活力總動員暑系列答案 龍人圖書快樂假期暑假作業鄭州大學出版社系列答案
龍人圖書快樂假期暑假作業鄭州大學出版社系列答案