
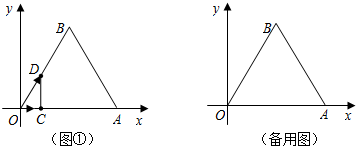
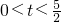 時,證明DC⊥OA;
時,證明DC⊥OA;
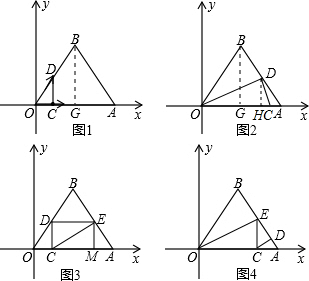 、解:(1)作BG⊥OA于G.
、解:(1)作BG⊥OA于G.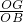 =cos∠BOA=cos60°=
=cos∠BOA=cos60°= ,
, =
= ,
,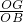 =
= ,
, 時,
時, =
= t,
t, ×OC×CD=
×OC×CD= ×t×
×t× t=
t= t2;
t2; ≤t<5時(如圖2)
≤t<5時(如圖2) =
= (5-t),
(5-t), ×OC×HD=
×OC×HD= ×t×
×t× (5-t)=
(5-t)= t-
t- t2;
t2; AC=
AC=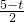 ,
,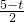 =5,
=5,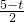 =2.
=2. =
= ,
, =1,OM=OA-AM=4.
=1,OM=OA-AM=4. );
); AB=
AB= ,
, ,
, ,
,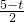 =
= ,
, ×
× =
=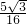 ,
, ×
× =
=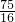 ,
,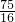 ,
,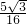 );
); )或(
)或(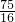 ,
,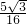 );
); GH•h,S△FGH=
GH•h,S△FGH= GH•h,
GH•h,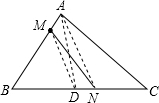
 時,點C不過OA中點,想證明垂直應(yīng)先作出一條和CD有關(guān)的垂線,利用相似求解;
時,點C不過OA中點,想證明垂直應(yīng)先作出一條和CD有關(guān)的垂線,利用相似求解; 時,和
時,和 ≤t<5時兩種情況探討,應(yīng)用t表示利用特殊的三角函數(shù)表示出OC邊上的高.進而表示出面積即可.
≤t<5時兩種情況探討,應(yīng)用t表示利用特殊的三角函數(shù)表示出OC邊上的高.進而表示出面積即可.

科目:初中數(shù)學 來源: 題型:
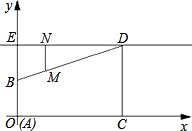 橫坐標為x,縱坐標為y.
橫坐標為x,縱坐標為y.查看答案和解析>>
科目:初中數(shù)學 來源: 題型:

查看答案和解析>>
科目:初中數(shù)學 來源: 題型:

查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
| 1 | 3 |

查看答案和解析>>
科目:初中數(shù)學 來源: 題型:解答題
 相交于點C.
相交于點C.
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com