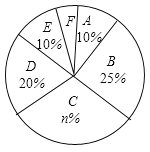
【題目】某校有
名學生，為了解全校學生的上學方式，該校數學興趣小組以問卷調查的形式，隨機調查了該校部分學生的主要上學方式(參與問卷調查的學生只能從以下六個種類中選擇一類)，并將調查結果繪制成如下不完整的統計圖．
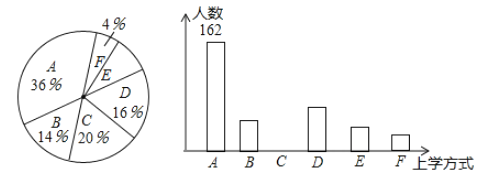
根據以上信息，回答下列問題：
（1）參與本次問卷調查的學生共有_____人，其中選擇
類的人數有_____人；
（2）在扇形統計圖中，求
類對應的扇形圓心角
的度數，并補全條形統計圖；
（3）若將
這四類上學方式視為“綠色出行”，請估計該校選擇“綠色出行”的學生人數．
【答案】（1）450，63；（2）
，補全的條形統計圖見解析；（3）該校選擇“綠色出行”的學生人數為2460人．
【解析】
（1）根據A類學生的扇形統計圖和條形統計圖的信息可得參與調查的總人數，再乘以B類學生的占比可得選擇B類的人數；
（2）根據扇形統計圖的定義得出E類學生的占比，從而可得其圓心角的度數，根據（1）的答案和扇形統計圖先求出
類學生的人數，再補全條形統計圖即可；
（3）先求出“綠色出行”的上學方式的占比，再乘以
即可．
（1）參與本次問卷調查的學生總人數為
（人）
選擇
類的人數為
（人）
故答案為：450，63；
（2）E類學生的占比為
則
類對應的扇形圓心角
的度數為
選擇C類學生的人數為
（人）
選擇D類學生的人數為
（人）
選擇E類學生的人數為
（人）
選擇F類學生的人數為
（人）
補全條形統計圖如下所示：
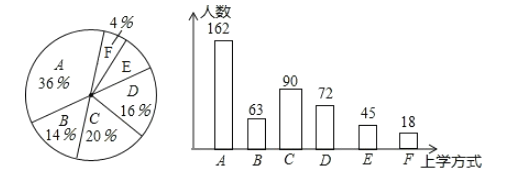
（3）由題意得：“綠色出行”的上學方式的占比為
則該校選擇“綠色出行”的學生人數為
（人）
答：該校選擇“綠色出行”的學生人數為2460人．
科目：初中數學 來源： 題型：
【題目】一次安全知識測驗中，學生得分均為整數，滿分10分，成績達到9分為優秀，這次測驗中甲、乙兩組學生人數相同，成績如下統計圖：
（1）在乙組學生成績統計圖中，8分所在的扇形的圓心角為___________度
（2）請補充完整下面的成績統計分析表：
平均數 | 方差 | 眾數 | 中位數 | 優秀率 | |
甲組 | 7 | 1.8 | 7 | 7 |
|
乙組 | 1.36 |
|
（3）你認為那組成績較好？從以上信息中寫出兩條支持你的選擇
（4）從甲、乙兩組得9分的學生中抽取兩人參加市級比賽，求這兩人來自不同組的概率
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，有四張背面完全相同的紙牌
，其正面分別畫有四個不同的幾何圖形，將這四張紙牌背面朝上洗勻.
（1）從中隨機摸出一張，求摸出的牌面圖形是中心對稱圖形的概率；
（2）小明和小亮約定做一個游戲，其規則為：先由小明隨機摸出一張紙牌，不放回，再由小亮從剩下的紙牌中隨機摸出一張，若摸出的兩張牌面圖形都是軸對稱圖形小明獲勝，否則小亮獲勝，這個游戲公平嗎？請用列表法（或樹狀圖）說明理由（紙牌用表示）.
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】小亮和爸爸登山，兩人距地面的高度
（米）與小亮登山時間
（分）之間的函數圖象分別如圖中折線
和線段
所示，根據函數圖形進行一下探究：
（1）設線段所表示的函數關系式為
，根據圖象求
的值，并寫出的實際意義；
（2）若小亮提速后，他登山的速度是爸爸速度的3倍，問：小亮登山多長時間時開始提速？此時小亮距地面的高度是多少米？
查看答案和解析>>
科目：初中數學 來源： 題型：
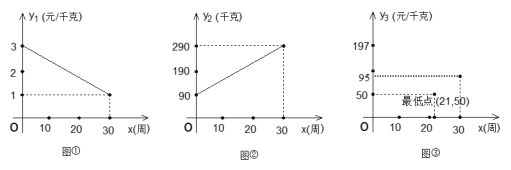
【題目】某水產基地種植某種食用海藻，從三月一日起的30周內，它的市場價格與上市時間的關系用圖①線段表示；它的平均畝產量與時間的關系用圖②線段表示；它的每畝平均成本與上市時間的關系用圖③拋物線表示．
（1）寫出圖①、圖②所表示的函數關系式；
（2）若市場價×畝產量－畝平均成本 = 每畝總利潤，問哪一周上市的海藻利潤最大？最大利潤是多少？
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，在⊙O中，點C為
的中點，∠ACB＝120°，OC的延長線與AD交于點D，且∠D＝∠B．
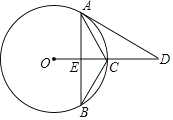
（1）求證：AD與⊙O相切；
（2）若CE＝4，求弦AB的長．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】某校為了解學生的每周平均課外閱讀時間，在本校隨機抽取若干名學生進行調查，并將調查結果繪制成如下不完整的統計圖表，請根據圖表中所給的信息解答下列問題：
組別 | 閱讀時間 | 頻數（人數） |
|
| 8 |
|
| 20 |
|
| 24 |
|
|
|
|
|
|
|
| 4 |
（1）圖表中的
______，
______；
（2）扇形統計圖中
組所對應的圓心角為______度；
（3）該校共有學生1500名，請估計該校有多少名學生的每周平均課外閱讀時間不低于3小時？
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖1,在平面直角坐標系中,直線
與拋物線
交于
兩點，其中
,
.該拋物線與
軸交于點
,與
軸交于另一點
.
(1)求
的值及該拋物線的解析式;
(2)如圖2.若點
為線段
上的一動點(不與
重合).分別以
、
為斜邊,在直線的同側作等腰直角△
和等腰直角△
,連接
,試確定△
面積最大時點的坐標.
(3)如圖3.連接
、
,在線段上是否存在點
,使得以
為頂點的三角形與△
相似,若存在,請直接寫出點的坐標;若不存在,請說明理由.
查看答案和解析>>
科目：初中數學 來源： 題型：
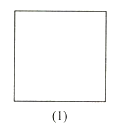
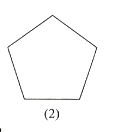
【題目】試比較圖中兩個幾何圖形的異同，請分別寫出它們的兩個相同點和兩個不同點。例如，相同點：正方形的對角線相等，正五邊形的。對角線也相等；不同點：正方形是中心對稱圖形，正五邊形不是中心對稱圖形。
相同點：①_________________；②___________________
不同點：①______________________；②____________________.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
