
【題目】在梯形ABCD中,AD∥BC,對角線AC和BD交于點O,下列條件中,能判斷梯形ABCD是等腰梯形的是( )
A.∠BDC =∠BCD
B.∠ABC =∠DAB
C.∠ADB =∠DAC
D.∠AOB =∠BOC
【答案】C
【解析】根據等腰梯形的判定,逐一作出判斷: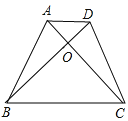
A.由∠BDC =∠BCD只能判斷△BCD是等腰三角形,而不能判斷梯形ABCD是等腰梯形;
B.由∠ABC =∠DAB和AD∥BC,可得∠ABC =∠DAB=900 , 是直角梯形,而不能判斷梯形ABCD是等腰梯形;
C.由∠ADB =∠DAC,可得AO=OD,由AD∥BC,可得∠ADB =∠DBC,∠DAC =∠ACB,從而得到∠DBC =∠ACB,所以OB=OC,因此AC=DB,根據對角線相等的梯形是等腰梯形可判定梯形ABCD是等腰梯形;
D.由∠AOB =∠BOC只能判斷梯形ABCD的對角線互相垂直,而不能判斷梯形ABCD是等腰梯形。
故選C.
【考點精析】關于本題考查的等腰三角形的判定和等腰梯形的性質,需要了解如果一個三角形有兩個角相等,那么這兩個角所對的邊也相等(簡稱:等角對等邊).這個判定定理常用于證明同一個三角形中的邊相等;等腰梯形的兩腰相等;同一底上的兩個角相等;兩條對角線相等才能得出正確答案.


 靈星計算小達人系列答案
靈星計算小達人系列答案 孟建平錯題本系列答案
孟建平錯題本系列答案科目:初中數學 來源: 題型:
【題目】如圖,在菱形ABCD中,AB=2,∠DAB=60°,點E是AD邊的中點,點M是AB邊上一動點(不與點A重合),延長ME交射線CD于點N,連接MD,AN.

(1)求證:四邊形AMDN是平行四邊形;
(2)填空:①當AM的值為 時,四邊形AMDN是矩形;②當AM的值為 時,四邊形AMDN是菱形。
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某生物課外活動小組的同學進行植物標本制作比賽,結果統計如下表:
每人所制 作標本數 | 2 | 4 | 6 | 8 | 10 |
人數 | 1 | 2 | 4 | 3 | 2 |
請根據表中信息,回答下列問題:
(1)該活動小組共有學生多少人?
(2)制作標本數在6個及以上的人數占小組總人數的百分比是多少?
(3)根據統計表制作一個合適的統計圖來描述這次比賽的結果.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】張華想用一塊面積為400cm2的正方形紙片,沿著邊的方向剪出一塊面積為300cm2的長方形紙片,使它的長寬之比為3:2.他不知能否裁得出來,正在發愁.李明見了說:“別發愁,一定能用一塊面積大的紙片裁出一塊面積小的紙片.”你同意李明的說法嗎?張華能用這塊紙片裁出符合要求的紙片嗎?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】知識背景:過中心對稱圖形的對稱中心的任意一條直線都將其分成全等的兩個部分.
(1)如圖①,直線m經過平行四邊形ABCD對角線的交點O,則S四邊形AEFB S四邊形DEFC(填“>”“<”“=”);
(2)如圖②,兩個正方形如圖所示擺放,O為小正方形對角線的交點,求作過點O的直線將整個圖形分成面積相等的兩部分;
(3)八個大小相同的正方形如圖③所示擺放,求作直線將整個圖形分成面積相等的兩部分(用三種方法分割).

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,將一條長為60 cm的卷尺鋪平后折疊,使得卷尺自身的一部分重合,然后在重合部分(陰影處)沿與卷尺邊垂直的方向剪一刀,此時卷尺分成了三段,若這三段長度由短到長的比為1∶2∶3,則折痕對應的刻度有________種可能.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】為了貫徹落實中央提出的“厲行節約,反對浪費”的精神,某校學生自發組織了“保護水源,從我做起”的活動,學生們對我國“水資源問題”進行了調查,發現我國水資源越來越匱乏,可是人們的節約意識并不強.據查,僅某飲料廠每天從地下抽水達3500立方米左右.同學們采取問卷調查的方式,隨機調查了本校150名同學家庭人均月用水量和節水措施情況.以下是根據調查結果作出的部分統計圖:

請根據以上信息,解答以下問題:
(1)補全圖①和圖②;
(2)為提高人們的節水意識,請你寫出一條與圖②中已明確的節水措施不同的節水措施.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在△ABC中,∠ABC和∠ACB的平分線相交于點O,過點O作EF∥BC交AB于E,交AC于F,過點O作OD⊥AC于D,下列四個結論:

①EF=BE+CF;
②∠BOC=90°+![]() ∠A;
∠A;
③點O到△ABC各邊的距離相等;
④設OD=m,AE+AF=n,則![]() .
.
其中正確的結論是____.(填序號)
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com