
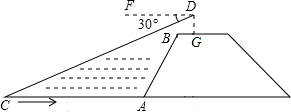
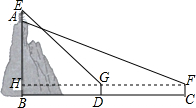
 如圖,小華站在河岸上的G點,看見河里有一小船沿垂直于岸邊的方向劃過來.此時測得小船C的俯角是∠FDC=30°.若小華的眼睛與地面的距離是$\sqrt{3}$米,BG=1.5米,BG平行于AC所在的直線,迎水坡i=4:3,坡長AB=10米,點A、B、C、D、F、G在同一平面內,則此時小船C到岸邊的距離CA的長是多少?(結果保留根號)
如圖,小華站在河岸上的G點,看見河里有一小船沿垂直于岸邊的方向劃過來.此時測得小船C的俯角是∠FDC=30°.若小華的眼睛與地面的距離是$\sqrt{3}$米,BG=1.5米,BG平行于AC所在的直線,迎水坡i=4:3,坡長AB=10米,點A、B、C、D、F、G在同一平面內,則此時小船C到岸邊的距離CA的長是多少?(結果保留根號) 分析 過點B作BE⊥AC于點E,延長DG交CA于點H,根據迎水坡AB的坡度i=4:3,坡長AB=10米,得出DH,CH的長,進而利用tan∠DCH=$\frac{DH}{CH}$=tan30°,求出CA即可.
解答 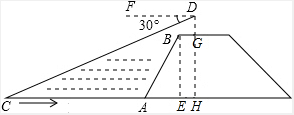 解:過點B作BE⊥AC于點E,延長DG交CA于點H,得Rt△ABE和矩形BEHG.
解:過點B作BE⊥AC于點E,延長DG交CA于點H,得Rt△ABE和矩形BEHG.
∵i=$\frac{BE}{AE}$=$\frac{4}{3}$,AB=10米,
∴BE=8,AE=6.
∵DG=$\sqrt{3}$,BG=1.5,
∴DH=DG+GH=$\sqrt{3}$+8,
AH=AE+EH=6+1.5=7.5.
在Rt△CDH中,
∵∠C=∠FDC=30°,DH=8+$\sqrt{3}$,tan30°=$\frac{DH}{CH}$=$\frac{8+\sqrt{3}}{CH}$=$\frac{\sqrt{3}}{3}$,
∴CH=8$\sqrt{3}$+3.
又∵CH=CA+7.5,
即8$\sqrt{3}$+3=CA+7.5,
∴CA=8$\sqrt{3}$-4.5(米).
答:CA的長約是(8$\sqrt{3}$-4.5)米.
點評 此題考查了直角三角形的應用,用到的知識點是坡角的定義以及銳角三角函數的應用,根據已知構造直角三角形得出tan∠DCH=$\frac{DH}{CH}$是本題的關鍵.


科目:初中數學 來源: 題型:解答題
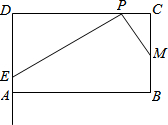 如圖,在矩形ABCD中,AB=m,BC=4,點M為邊BC的中點,點P為邊CD上的動點(點P異于C,D兩點).連接PM,過點P作PM的垂線與射線DA相交于點E(如圖).
如圖,在矩形ABCD中,AB=m,BC=4,點M為邊BC的中點,點P為邊CD上的動點(點P異于C,D兩點).連接PM,過點P作PM的垂線與射線DA相交于點E(如圖).查看答案和解析>>
科目:初中數學 來源: 題型:填空題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
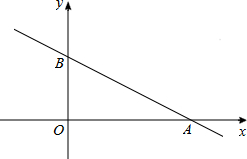 如圖,在以點O為原點的直角坐標系中,一次函數y=-$\frac{1}{2}$x+1的圖象與x軸交于A,與y軸交于點B,求:
如圖,在以點O為原點的直角坐標系中,一次函數y=-$\frac{1}{2}$x+1的圖象與x軸交于A,與y軸交于點B,求:查看答案和解析>>
科目:初中數學 來源: 題型:解答題
 數學實踐活動小組實地測量山峰與山下廣場的相對高度AB,器測量步驟如下:
數學實踐活動小組實地測量山峰與山下廣場的相對高度AB,器測量步驟如下:查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | $\frac{1}{2}$ | B. | 1 | C. | $\frac{4}{3}$ | D. | 2 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com