
【題目】“構造圖形解題”,它的應用十分廣泛,特別是有些技巧性很強的題目,如果不能發現題目中所隱含的幾何意義,而用通常的代數方法去思考,經常讓我們手足無措,難以下手,這時,如果能轉換思維,發現題目中隱含的幾何條件,通過構造適合的幾何圖形,將會得到事半功倍的效果,下面介紹兩則實例:
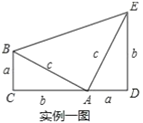
實例一:1876年,美國總統伽非爾德利用實例一圖證明了勾股定理:由![]() 四邊形
四邊形![]() 得
得![]() ,化簡得:
,化簡得:![]() .
.
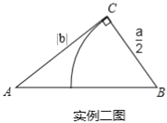
實例二:歐幾里得的《幾何原本》記載,關于![]() 的方程
的方程![]() 的圖解法是:畫
的圖解法是:畫![]() ,使
,使![]() ,
,![]() ,
,![]() ,再在斜邊
,再在斜邊![]() 上截取
上截取![]() ,則
,則![]() 的長就是該方程的一個正根(如實例二圖).
的長就是該方程的一個正根(如實例二圖).
根據以上閱讀材料回答下面的問題:
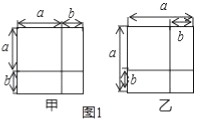
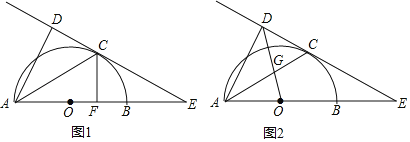
(1)如圖1,請利用圖形中面積的等量關系,寫出甲圖要證明的數學公式是 ,乙圖要證明的數學公式是 ,體現的數學思想是 ;
(2)如圖2,按照實例二的方式構造![]() ,連接
,連接![]() ,請用含字母
,請用含字母![]() 、
、![]() 的代數式表示
的代數式表示![]() 的長,
的長,![]() 的表達式能和已學的什么知識相聯系;
的表達式能和已學的什么知識相聯系;
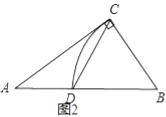
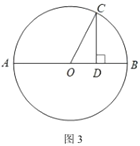
(3)如圖3,已知![]() ,
,![]() 為直徑,點
為直徑,點![]() 為圓上一點,過點
為圓上一點,過點![]() 作
作![]() 于點
于點![]() ,連接
,連接![]() ,設
,設![]() ,
,![]() ,求證:
,求證:![]() .
.
【答案】(1)完全平方公式,平方差公式,數形結合的思想;(2)![]() ,
,![]() 的表達式能和一元二次方程的求根公式相聯系;(3)證明見解析.
的表達式能和一元二次方程的求根公式相聯系;(3)證明見解析.
【解析】
(1)根據大正方形面積=各個部分面積之和,即可得到完全平方公式和平方差公式,進而即可得到答案;
(2)根據勾股定理以及一元二次方程的求根公式,即可得到答案;
(3)連接![]() ,
,![]() ,易證
,易證![]() ,
,![]() ,結合
,結合![]()
![]() ,即可得到結論.
,即可得到結論.
(1)如圖1中,圖甲大正方形的面積![]() ,
,
圖乙中大正方形的面積![]() ,即:
,即:![]() .
.
它們都體現了數形結合的思想.
故答案是:完全平方公式,平方差公式,數形結合的思想;
(2)∵在![]() 中,
中,![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ;
;
解![]() ,由求根公式可得
,由求根公式可得![]() ,
,
答:![]() 的表達式能和一元二次方程的求根公式相聯系;
的表達式能和一元二次方程的求根公式相聯系;
(3)由已知,可得![]() ,連接
,連接![]() ,
,![]() .
.
∵![]() 為直徑,
為直徑,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,即
,即![]() ,
,
∵在![]() 中,
中,![]() ,
,
∴![]() ,即
,即![]() ,
,
∴![]() .
.


科目:初中數學 來源: 題型:
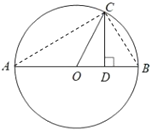
【題目】(新洲區月考)如圖1,AB為半圓O的直徑,C為圓弧上一點,過點C的直線與AB的延長線交于點E,AD⊥CE于點D,AC平分∠DAB.
(1)求證:CE是⊙O的切線.
(2)若AB=6,B為OE的中點,CF⊥AB,垂足為點F,求CF的長;
(3)如圖2,連接OD交AC于點G,若![]() ,求sinE的值.
,求sinE的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
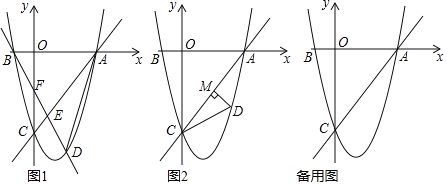
【題目】如圖,在平面直角坐標系中,直線y=![]() x﹣4與拋物線y=
x﹣4與拋物線y=![]() +bx+c交于坐標軸上兩點A、C,拋物線與x軸另一交點為點B;
+bx+c交于坐標軸上兩點A、C,拋物線與x軸另一交點為點B;
(1)求拋物線解析式;
(2)若動點D在直線AC下方的拋物線上;
①作直線BD,交線段AC于點E,交y軸于點F,連接AD;求△ADE與△CEF面積差的最大值,及此時點D的坐標;
②如圖2,作DM⊥直線AC,垂足為點M,是否存在點D,使△CDM中某個角恰好是∠ACO的一半?若存在,直接寫出點D的橫坐標;若不存在,說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
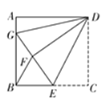
【題目】如圖,在正方形ABCD中,點E是BC邊的中點,將△DCE沿DE折疊,使點C落在點F處,延長EF交AB于點G,連接DG、BF.
(1)求證:DG平分∠ADF;
(2)若AB=12,求△EDG的面積.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】距離中考體考時間越來越近,年級想了解初三年級1512名學生周末在家體育鍛煉的情況,在初三年級隨機抽取了18名男生和18名女生,對他們周末在家的鍛煉時間進行了調查,并收集得到了以下數據(單位:分鐘)
男生:28,30,32,46,68,39,80,70,66,57,70,95,100,58,69,88,99,105
女生:36,48,78,99,56,62,35,109,29,88,88,69,73,55,90,98,69,72
統計數據,并制作了如下統計表:
時間 |
|
|
|
|
男生 | 2 |
|
| 4 |
女生 | 1 | 5 | 9 | 3 |
分析數據:兩組數據的極差、平均數、中位數、眾數如表所示
極差 | 平均數 | 中位數 | 方差 | ||
男生 | 77 | 66.7 |
| 70 | 617.3 |
女生 |
| 69.7 | 70.5 |
| 547.2 |
(1)請將上面的表格補充完整:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ;
;
(2)已知該年級男女生人數差不多,根據調查的數據,估計初三年級周末在家鍛煉的時間在90分鐘以上(不包含90分鐘)的同學約有多少人?
(3)體育老師看了表格數據后認為初三年級的女生周末鍛煉做得比男生好,請你結合統計數據,寫出兩條支持體育老師觀點的理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】時下娛樂綜藝節目風靡全國,隨機對九年級部分學生進行了一次調查,對最喜歡《我是喜劇王》(記為A)、《王牌對王牌》(記為B)、《奔跑吧,兄弟》(記為C)、《歡樂喜劇人》(記為D)的同學進行了統計(每位同學只選擇一個最喜歡的節目),繪制了以下不完整的統計圖,請根據圖中信息解答問題:
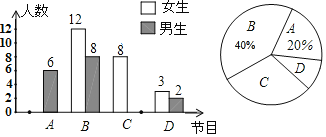
(1)求本次調查一共選取了多少名學生;
(2)將條形統計圖補充完整;
(3)若九年級共有1900名學生,估計其中最喜歡《奔跑吧,兄弟》的學生大約是多少名.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,AB是⊙O的直徑,BC交⊙O于點D,E是![]() 的中點,連接AE交BC于點F,∠ACB=2∠EAB.
的中點,連接AE交BC于點F,∠ACB=2∠EAB.

(1)求證:AC是⊙O的切線;
(2)若cosC=![]() ,AC=6,求BF的長.
,AC=6,求BF的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】二次函數y=ax2+bx+c(a≠0)的圖象如圖所示,有下列結論:①abc>0;②2a+b=0;③若m為任意實數,則a+b>am2+bm;④a﹣b+c>0;⑤若ax12+bx1=ax22+bx2,且x1≠x2,則x1+x2=2.其中,正確結論的個數為( )
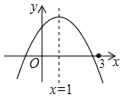
A.1B.2C.3D.4
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,![]() 是
是![]() 的直徑,
的直徑,![]() 是
是![]() 上一點,過
上一點,過![]() 作
作![]() 的切線,交
的切線,交![]() 的延長線于點
的延長線于點![]() ,過
,過![]() 作
作![]() ,交
,交![]() 延長線于點
延長線于點![]() ,連接
,連接![]() ,交
,交![]() 于點
于點![]() ,交
,交![]() 于點
于點![]() ,連接
,連接![]() .
.
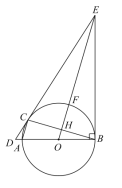
(1)求證:![]() ;
;
(2)連接![]() ,若
,若![]() ,
,![]() ,求
,求![]() 的長.
的長.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com