

 (BE+CF),由于△PBC是等腰直角三角形,故PI=BI=CI,再根據(jù)三角形的面積公式即可得出結(jié)論;
(BE+CF),由于△PBC是等腰直角三角形,故PI=BI=CI,再根據(jù)三角形的面積公式即可得出結(jié)論;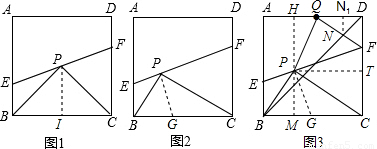 解:(1)如圖1所示:過點P作PI⊥BC于點I,
解:(1)如圖1所示:過點P作PI⊥BC于點I, (BE+CF),
(BE+CF), BE•BI+
BE•BI+ CF•CI=
CF•CI= BE×
BE× BC+
BC+ CF•
CF• BC=
BC= BC(BE+CF)=
BC(BE+CF)= BC•PI=S△PBC;
BC•PI=S△PBC;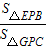 =(
=(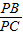 )2=
)2=
 •
•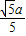 •
•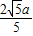 =80,解得a=20,
=80,解得a=20,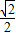 QD=2
QD=2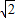 ;
;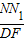 =
=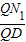 ,
,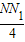 =
=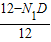 ,解得NN1=3,
,解得NN1=3,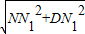 =
=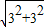 =3
=3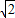 ,
,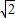 或3
或3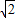 .
.

 新課標(biāo)階梯閱讀訓(xùn)練系列答案
新課標(biāo)階梯閱讀訓(xùn)練系列答案科目:初中數(shù)學(xué) 來源: 題型:

查看答案和解析>>
科目:初中數(shù)學(xué) 來源:2013年初中數(shù)學(xué)單元提優(yōu)測試卷-相似的判定解答題(帶解析) 題型:解答題
已知:點P為正方形ABCD內(nèi)部一點,且∠BPC=90°,過點P的直線分別交邊AB、邊CD于點E、點F.
(1)如圖1,當(dāng)PC=PB時,則S△PBE、S△PCF S△BPC之間的數(shù)量關(guān)系為 _________ ;
(2)如圖2,當(dāng)PC=2PB時,求證:16S△PBE+S△PCF=4S△BPG;
(3)在(2)的條件下,Q為AD邊上一點,且∠PQF=90°,連接BD,BD交QF于點N,若S△bpc=80,BE=6.求線段DN的長.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源:2013年初中數(shù)學(xué)單元提優(yōu)測試卷-相似的判定解答題(解析版) 題型:解答題
已知:點P為正方形ABCD內(nèi)部一點,且∠BPC=90°,過點P的直線分別交邊AB、邊CD于點E、點F.
(1)如圖1,當(dāng)PC=PB時,則S△PBE、S△PCF S△BPC之間的數(shù)量關(guān)系為 _________ ;
(2)如圖2,當(dāng)PC=2PB時,求證:16S△PBE+S△PCF=4S△BPG;
(3)在(2)的條件下,Q為AD邊上一點,且∠PQF=90°,連接BD,BD交QF于點N,若S△bpc=80,BE=6.求線段DN的長.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:解答題

查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com