
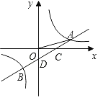
【題目】如圖,一次函數![]() 的圖象與反比例函數
的圖象與反比例函數![]() 的圖象交于
的圖象交于![]() ,
,![]() 兩點,與
兩點,與![]() 軸交于點
軸交于點![]() ,與
,與![]() 軸交于點
軸交于點![]() ,已知
,已知![]() ,
,![]() ,點
,點![]() 的坐標為
的坐標為![]() .
.
![]() 求反比例函數的解析式;
求反比例函數的解析式;
![]() 求一次函數的解析式;
求一次函數的解析式;
![]() 在
在![]() 軸上存在一點
軸上存在一點![]() ,使得
,使得![]() 與
與![]() 相似,請你求出
相似,請你求出![]() 點的坐標.
點的坐標.
【答案】![]()
![]() ;
;![]()
![]() 點坐標為
點坐標為![]() .
.
【解析】
(1)中,因為OA=![]() ,tan∠AOC=
,tan∠AOC=![]() ,則可過A作AE垂直x軸,垂足為E,利用三角函數和勾股定理即可求出AE=1,OE=3,從而可知A(3,1),又因點A在反比例函數y=
,則可過A作AE垂直x軸,垂足為E,利用三角函數和勾股定理即可求出AE=1,OE=3,從而可知A(3,1),又因點A在反比例函數y=![]() 的圖象上,由此可求出開k=3,從而求出反比例函數的解析式;
的圖象上,由此可求出開k=3,從而求出反比例函數的解析式;
(2)中,因為一次函數y=ax+b的圖象與反比例函數y=![]() 的圖象交于A,B兩點,點B的坐標為(m,2).所以3=2x.即m=
的圖象交于A,B兩點,點B的坐標為(m,2).所以3=2x.即m=![]() ,B(
,B(![]() ,2).然后把點A、B的坐標代入一次函數的解析式,得到關于a、b的方程組,解之即可求出a、b的值,最終寫出一次函數的解析式;
,2).然后把點A、B的坐標代入一次函數的解析式,得到關于a、b的方程組,解之即可求出a、b的值,最終寫出一次函數的解析式;
(3)因為在y軸上存在一點P,使得△PDC與△ODC相似,而∠PDC和∠ODC是公共角,所以有△PDC∽△CDO,![]() ,,而點C、D分別是一次函數y=
,,而點C、D分別是一次函數y=![]() x1的圖象與x軸、y軸的交點,因此有C(
x1的圖象與x軸、y軸的交點,因此有C(![]() ,0)、D(0,1).OC=
,0)、D(0,1).OC=![]() ,OD=1,DC=
,OD=1,DC=![]() .進而可求出PD=
.進而可求出PD=![]() ,OP=
,OP=![]() .寫出點P的坐標.
.寫出點P的坐標.
![]() 過
過![]() 作
作![]() 垂直
垂直![]() 軸,垂足為
軸,垂足為![]() ,
,
∵![]() ,
,
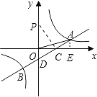
∴![]() ,
,
∵![]() ,
,![]() ,
,
∴![]() ,
,![]() ,
,
∴點![]() 的坐標為
的坐標為![]() .
.
∵![]() 點在雙曲線上,
點在雙曲線上,
∴![]() ,
,
∴![]() .
.
∴雙曲線的解析式為![]() ;
;
![]() ∵點
∵點![]() 在雙曲線
在雙曲線![]() 上,
上,
∴![]() ,
,
∴![]() .
.
∴點![]() 的坐標為
的坐標為![]() .
.
∴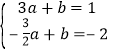 ,∴
,∴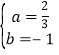 ,
,
∴一次函數的解析式為![]() ;
;
![]() 過點
過點![]() 作
作![]() ,交
,交![]() 軸于點
軸于點![]() ,
,
∵![]() ,
,![]() 兩點在直線
兩點在直線![]() 上,
上,
∴![]() ,
,![]() 的坐標分別是:
的坐標分別是:![]() ,
,![]() .
.
即:![]() ,
,![]() ,
,
∴![]() .
.
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
又![]() ,
,
∴![]() 點坐標為
點坐標為![]() .
.


科目:初中數學 來源: 題型:
【題目】有下列六個命題:①相等的角是對頂角;②兩直線平行,同位角相等;③若一個三角形的兩個內角分別為![]() 和
和![]() ,則這個三角形是直角三角形;④全等三角形的對應角相等。其中逆命題是假命題的個數有( )
,則這個三角形是直角三角形;④全等三角形的對應角相等。其中逆命題是假命題的個數有( )
A.0個B.1個C.2個D.3個
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在△ABC中,AD是∠BAC的平分線,AD的垂線平分線交AB于點F,交BC的延長線于點E,連接AE,DF.
求證:(1)∠EAD=∠EDA;(2)DF//AC;(3)∠EAC=∠B.

查看答案和解析>>
科目:初中數學 來源: 題型:
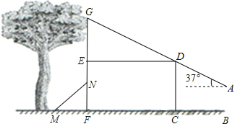
【題目】身高![]() 米的兵兵在建筑物前放風箏,風箏不小心掛在了樹上.在如圖所示的平面圖形中,矩形
米的兵兵在建筑物前放風箏,風箏不小心掛在了樹上.在如圖所示的平面圖形中,矩形![]() 代表建筑物,兵兵位于建筑物前點
代表建筑物,兵兵位于建筑物前點![]() 處,風箏掛在建筑物上方的樹枝點
處,風箏掛在建筑物上方的樹枝點![]() 處(點
處(點![]() 在
在![]() 的延長線上).經測量,兵兵與建筑物的距離
的延長線上).經測量,兵兵與建筑物的距離![]() 米,建筑物底部寬
米,建筑物底部寬![]() 米,風箏所在點
米,風箏所在點![]() 與建筑物頂點
與建筑物頂點![]() 及風箏線在手中的點
及風箏線在手中的點![]() 在同一條直線上,點
在同一條直線上,點![]() 距地面的高度
距地面的高度![]() 米,風箏線與水平線夾角為
米,風箏線與水平線夾角為![]() .
.
![]() 求風箏距地面的高度
求風箏距地面的高度![]() ;
;
![]() 在建筑物后面有長
在建筑物后面有長![]() 米的梯子
米的梯子![]() ,梯腳
,梯腳![]() 在距墻
在距墻![]() 米處固定擺放,通過計算說明:若兵兵充分利用梯子和一根
米處固定擺放,通過計算說明:若兵兵充分利用梯子和一根![]() 米長的竹竿能否觸到掛在樹上的風箏?
米長的竹竿能否觸到掛在樹上的風箏?
(參考數據:![]() ,
,![]() ,
,![]() )
)
查看答案和解析>>
科目:初中數學 來源: 題型:
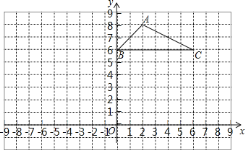
【題目】如圖,方格紙中每個小格的邊長均為![]() ,
,![]() 的頂點都在格點上,建立平面直角坐標系.
的頂點都在格點上,建立平面直角坐標系.
![]() 點
點![]() 的坐標是________,點
的坐標是________,點![]() 的坐標是________;
的坐標是________;
![]() 以原點
以原點![]() 為位似中心,將
為位似中心,將![]() 縮小,使變換后的到的
縮小,使變換后的到的![]() 與
與![]() 對應邊的比為
對應邊的比為![]() 請在網格中畫出
請在網格中畫出![]() ,并寫出
,并寫出![]() 的面積為________.
的面積為________.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在Rt△ABC中,∠C=90°,a,b,c分別是∠A、∠B、∠C的對邊
(1)若a=![]() ,c=4,求b
,c=4,求b
(2)若c=8,∠A=30°,求b
(3)若a:b=3:4,c=15,求Rt△ABC的面積.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在△ABC,AB=AC,DE⊥AB于點E,DF⊥AC于點F,BD=CD
求證:DE=DF

證明:∵AB=AC
∴∠B=∠C( ),
∵DE⊥AB,DF⊥AC
∴∠BED=∠DFC=90°
在△BDE和△CDF中

∴△BDE≌△CDF( ).
∴DE=DF( )
(1)請在括號里寫出推理的依據.
(2)請你寫出另一種證明此題的方法.
查看答案和解析>>
科目:初中數學 來源: 題型:
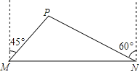
【題目】我市準備在相距![]() 千米的
千米的![]() ,
,![]() 兩工廠間修一條筆直的公路,但在
兩工廠間修一條筆直的公路,但在![]() 地北偏東
地北偏東![]() 方向、
方向、![]() 地北偏西
地北偏西![]() 方向的
方向的![]() 處,有一個半徑為
處,有一個半徑為![]() 千米的住宅小區(如圖),問修筑公路時,這個小區是否有居民需要搬遷?(參考數據:
千米的住宅小區(如圖),問修筑公路時,這個小區是否有居民需要搬遷?(參考數據:![]() ,
,![]() )
)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】圖①是一個長為2m,寬為2n的長方形,沿圖中虛線用剪刀均勻分成四塊小長方形,然后按圖②形狀拼成一個正方形.

(1)請用兩種不同方法,求②中陰影部分的面積(不用化簡)
方法1: ;方法2: ;
(2)觀察圖②,寫出(m+n)2,(m﹣n)2,mn之間的等量關系 ;
(3)根據(2)題中的等量關系,解決如下問題:
①若a+b=7,ab=5,求(a﹣b)2的值;
②若2a+b=5,ab=2,求2a﹣b的值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com