
【題目】如圖,直線AB、CD相交于點O,OF平分∠AOE,OF⊥CD,垂足為O.
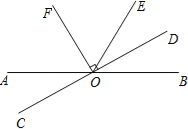
(1)若∠AOE=120°,求∠BOD的度數;
(2)寫出圖中所有與∠AOD互補的角: .
【答案】(1)30°;(2)∠AOC、∠BOD、∠DOE.
【解析】試題分析:(1)根據角平分線的性質可得∠AOF=![]() ∠AOE=60°,再由OF⊥CD,可得∠COF=90°,再根據角的和差關系可得∠AOC的度數,根據對頂角相等可得答案;
∠AOE=60°,再由OF⊥CD,可得∠COF=90°,再根據角的和差關系可得∠AOC的度數,根據對頂角相等可得答案;
(2)根據兩個角的和為180°即為互補可得答案.
解:(1)∵OF平分∠AOE,∠AOE=120°,
∴∠AOF=![]() ∠AOE=60°.
∠AOE=60°.
∵OF⊥CD,
∴∠COF=90°,
∴∠AOC=∠COF﹣∠AOF=30°,
∵∠AOC和∠BOD是對頂角,
∴∠BOD=∠AOC=30°;
(2)與∠AOD互補的角有∠AOC、∠BOD、∠DOE,
故答案為:∠AOC、∠BOD、∠DOE.


科目:初中數學 來源: 題型:
【題目】一架方梯AB長25米,如圖所示,斜靠在一面上:

(1)若梯子底端離墻7米,這個梯子的頂端距地面有多高?
(2)在(1)的條件下,如果梯子的頂端下滑了4米,那么梯子的底端在水平方向滑動了幾米?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某市從今年1月1日起調整水價,每立方米水費上漲了原價的![]() .據了解,某校去年11月份的水費是1800元,而今年1月份的水費是3600元.如果該校今年1月份的用水量比去年11月份的用水量多600m3.
.據了解,某校去年11月份的水費是1800元,而今年1月份的水費是3600元.如果該校今年1月份的用水量比去年11月份的用水量多600m3.
(1)該市原來每立方米水價是多少元?
(2)該校開展了“節約每一滴水”的主題活動,采取了有效的節約用水措施,計劃今年5月份的用水量較1月份降低20%,那么該校今年5月份應交的水費是多少?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】一輛汽車勻速通過某段公路,所需時間![]() 與行駛速度
與行駛速度![]() (km/h)滿足函數表達式
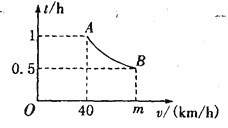
(km/h)滿足函數表達式![]() .其圖像為如圖所示的一段曲線,且端點為A(40,1)和B(
.其圖像為如圖所示的一段曲線,且端點為A(40,1)和B(![]() ,0.5)
,0.5)
(1)求k和m的值。
(2)若行駛速度不能超過60 km/h,則汽車通過該路段最少需要多長時間?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com