
【題目】如圖,1,將一張矩形紙片![]() 沿著對角線
沿著對角線![]() 向上折疊,頂點
向上折疊,頂點![]() 落到點
落到點![]() 處,
處,![]() 交
交![]() 于點
于點![]() .
.
(1)求證:![]() 是等腰三角形;
是等腰三角形;
(2)如圖2,過點![]() 作
作![]() ,交
,交![]() 于點
于點![]() ,連結
,連結![]() 交
交![]() 于點
于點![]() .
.
①判斷四邊形![]() 的形狀,并說明理由;
的形狀,并說明理由;
②若![]() ,
,![]() ,求
,求![]() 的長.
的長.

【答案】(1)證明見解析;(2) ![]() .
.
【解析】
試題分析: (1)根據兩直線平行內錯角相等及折疊特性判斷;
(2)①根據已知矩形性質及第一問證得鄰邊相等判斷;
②根據折疊特性設未知邊,構造勾股定理列方程求解.
試題解析:(1)證明:如圖1,根據折疊,∠DBC=∠DBE,

又AD∥BC,
∴∠DBC=∠ADB,
∴∠DBE=∠ADB,
∴DF=BF,
∴△BDF是等腰三角形;
(2)①∵四邊形ABCD是矩形,
∴AD∥BC,
∴FD∥BG,
又∵FD∥BG,
∴四邊形BFDG是平行四邊形,
∵DF=BF,
∴四邊形BFDG是菱形;
②∵AB=6,AD=8,
∴BD=10.
∴OB=![]() BD=5.
BD=5.
假設DF=BF=x,∴AF=AD﹣DF=8﹣x.
∴在直角△ABF中,AB2+A2=BF2,即62+(8﹣x)2=x2,
解得x=![]() ,
,
即BF=![]() ,
,
∴FO=![]() =
=![]() ,
,
∴FG=2FO=![]() .
.



 天天向上口算本系列答案
天天向上口算本系列答案科目:初中數學 來源: 題型:
【題目】如圖,矩形ABCD的對角線AC、BD交于點O,且DE∥AC,CE∥BD. 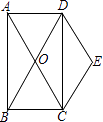
(1)求證:四邊形OCED是菱形;
(2)若∠BAC=30°,AC=4,求菱形OCED的面積.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,拋物線![]() 與直線
與直線![]() 交于
交于![]() ,
,![]() 兩點,直線
兩點,直線![]() 交
交![]() 軸與點
軸與點![]() ,點
,點![]() 是直線
是直線![]() 上的動點,過點
上的動點,過點![]() 作
作![]() 軸交
軸交![]() 于點
于點![]() ,交拋物線于點
,交拋物線于點![]() .
.
(1)求拋物線![]() 的表達式;
的表達式;
(2)連接![]() ,
,![]() ,當四邊形
,當四邊形![]() 是平行四邊形時,求點
是平行四邊形時,求點![]() 的坐標;
的坐標;
(3)①在![]() 軸上存在一點
軸上存在一點![]() ,連接
,連接![]() ,
,![]() ,當點
,當點![]() 運動到什么位置時,以
運動到什么位置時,以![]() 為頂點的四邊形是矩形?求出此時點
為頂點的四邊形是矩形?求出此時點![]() 的坐標;
的坐標;
②在①的前提下,以點![]() 為圓心,
為圓心,![]() 長為半徑作圓,點
長為半徑作圓,點![]() 為
為![]() 上一動點,求
上一動點,求![]() 的最小值.
的最小值.
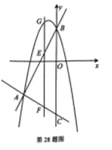
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在長方形ABCD中,AB=2,BC=1,動點P從點B出發,沿路線B→C→D做勻速運動,那么△ABP的面積S與點P運動的路程x之間的函數圖象大致為( )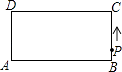
A.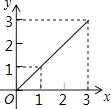
B.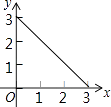
C.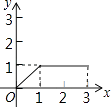
D.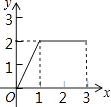
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在數學課上,同學們已經探究過“經過已知直線外一點作這條直線的垂線”的尺規作圖過程:
已知:直線
求作:直線 做法:如圖:(1)在直線 (2)分別以點 (3)作直線 |
參考以上材料作圖的方法,解決以下問題:
(1)以上材料作圖的依據是 .
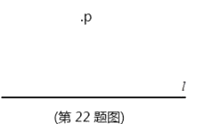
(3)已知:直線![]() 和
和![]() 外一點
外一點![]() ,
,
求作:![]() ,使它與直線
,使它與直線![]() 相切。(尺規作圖,不寫做法,保留作圖痕跡,并把作圖痕跡用黑色簽字筆描黑)
相切。(尺規作圖,不寫做法,保留作圖痕跡,并把作圖痕跡用黑色簽字筆描黑)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知二次函數![]() 的圖象與
的圖象與![]() 軸交于點
軸交于點![]() ,點
,點![]() ,與
,與![]() 軸交于點
軸交于點![]() .
.
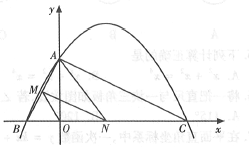
(1)求二次函數![]() 的表達式;
的表達式;
(2)連接![]() ,若點
,若點![]() 在線段
在線段![]() 上運動(不與點
上運動(不與點![]() 重合),過點
重合),過點![]() 作
作![]() ,交
,交![]() 于點
于點![]() ,當
,當![]() 面積最大時,求N點的坐標;
面積最大時,求N點的坐標;
(3)連接![]() ,在(2)的結論下,求
,在(2)的結論下,求![]() 與
與![]() 的數量關系.
的數量關系.
查看答案和解析>>
科目:初中數學 來源: 題型:
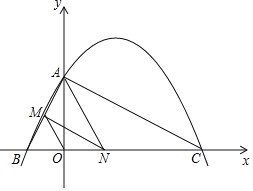
【題目】如圖,已知二次函數y=ax2+bx+4的圖象與x軸交于點B(-2,0),點C(8,0),與y軸交于點A.
(1)求二次函數y=ax2+bx+4的表達式;
(2)連接AC,AB,若點N在線段BC上運動(不與點B,C重合),過點N作NM∥AC,交AB于點M,當△AMN面積最大時,求N點的坐標;
(3)連接OM,在(2)的結論下,求OM與AC的數量關系.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com