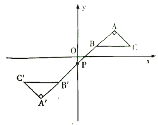
日日人人_亚洲美女在线视频_av手机在线播放_国产大片aaa_欧美中文日韩_午夜理伦三级

精英家教網 > 初中數學 > 題目詳情

【題目】如圖，在平面直角坐標系中，的頂點在第一象限，點、的坐標分別為、，，，直線交軸于點，若與關于點成中心對稱，則點的坐標為（ ）

A. B. C. D.

【答案】A

【解析】先求得直線AB解析式為y=x﹣1，即可得P（0，﹣1），再根據點A與點A'關于點P成中心對稱，利用中點坐標公式，即可得到點A'的坐標.

∵點B，C的坐標分別為（2，1），（6，1），∠BAC=90°，AB=AC，

∴△ABC是等腰直角三角形，

∴A（4，3），

設直線AB解析式為y=kx+b，

則，解得，

∴直線AB解析式為y=x﹣1，

令x=0，則y=﹣1，

∴P（0，﹣1），

又∵點A與點A'關于點P成中心對稱，

∴點P為AA'的中點，

設A'（m，n），則=0，=﹣1，

∴m=﹣4，n=﹣5，

∴A'（﹣4，﹣5），

故選：A．

練習冊系列答案
相關習題

科目：初中數學 來源： 題型：

【題目】解決問題：(假設行車過程沒有停車等時，且平均車速為0．5千米/分鐘)

華夏專車

神州專車

里程費

1.8元/千米

2元/千米

時長費

0.3元/分鐘

0.6元/分鐘

遠途費

0.8元/千米產（超過7千米部分）

無

起步價

無

10元

華夏專車：車費由里程費、時長費、遠途費三部分構成，其中里程費按行車的實際里程計算；時長費按行車的實際時間計算；遠途費的收取方式為：行車里程7千米以內（含7千米）不收遠途費，超過7千米的，超出的部分按每千米加收0.8元．

神州專車：車費由里程費、時長費、起步價三部分構成，其中里程費按行車的實際里程計算；時長費按行車的實際時間計算；起步價與行車距離無關．

（1）小明在該地區出差，乘車距離為10千米，如果小明使用華夏專車，需要支付的打車費用為 元；

（2）小強在該地區從甲地乘坐神州專車到乙地，一共花費42元，求甲乙兩地距離是多少千米？

（3）神州專車為了和華夏專車競爭客戶，分別推出了優惠方式，華夏專車對于乘車路程在7千米以上(含7千米)的客戶每次收費立減9元；神州打車車費5折優惠．對采用哪一種打車方式更合算提出你的建議．

查看答案和解析>>

科目：初中數學 來源： 題型：

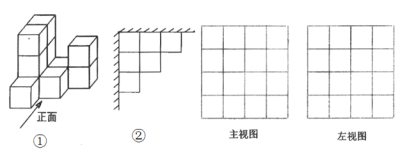
【題目】在平整的地面上，由若干個完全相同的棱長為10 cm的小正方體堆成一個幾何體，如圖①所示.

(1)請你在方格紙中分別畫出這個幾何體的主視圖和左視圖;

(2)若現在手頭還有一些相同的小正方體，如果保持這個幾何體的主視圖和俯視圖不變，

Ⅰ.在圖①所示幾何體上最多可以添加 個小正方體;

Ⅱ.在圖①所示幾何體上最多可以拿走 個小正方體;

Ⅲ.在題Ⅱ的情況下，把這個幾何體放置在墻角，使得幾何體的左面和后面靠墻，其俯視圖如圖②所示，若給該幾何體露在外面的面噴上紅漆，則需要噴漆的面積最少是多少平方厘米?

查看答案和解析>>

科目：初中數學 來源： 題型：

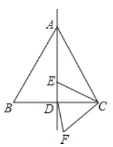
【題目】如圖，邊長為4的等邊三角形ABC中，E是對稱軸AD上的一個動點，連接EC，將線段EC繞點C逆時針旋轉60°得到FC，連接DF，則在點E運動過程中，DF的最小值是______.

查看答案和解析>>

科目：初中數學 來源： 題型：

【題目】如圖，AB＝16，O為AB中點，點C在線段OB上（不與點O，B重合），將OC繞點O逆時針旋轉270°后得到扇形COD，AP，BQ分別切優弧于點P，Q，且點P， Q在AB異側，連接OP．

（1）求證：AP＝BQ；

（2）當BQ＝4時，求扇形COQ的面積及的長（結果保留π）；

（3）若△APO的外心在扇形COD的內部，請直接寫出OC的取值范圍．

查看答案和解析>>

科目：初中數學 來源： 題型：

【題目】（理解新知）如圖①，已知，在內部畫射線，得到三個角，分別為，，，若這三個角中有一個角是另外一個角的兩倍，則稱射線為的“二倍角線”．

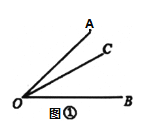
（1）一個角的角平分線______這個角的“二倍角線”（填“是”或“不是”）

（2）若，射線為的“二倍角線”，則的大小是______；

（解決問題）如圖②，己知，射線從出發，以/秒的速度繞點逆時針旋轉；射線從出發，以/秒的速度繞點順時針旋轉，射線，同時出發，當其中一條射線回到出發位置的時候，整個運動隨之停止，設運動的時間為秒．

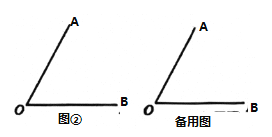
（3）當射線，旋轉到同一條直線上時，求的值；

（4）若，，三條射線中，一條射線恰好是以另外兩條射線為邊組成的角的“二倍角線”，直接寫出所有可能的值______．

查看答案和解析>>

科目：初中數學 來源： 題型：

【題目】求不等式（2x﹣1）（x+3）＞0的解集．

解：根據“同號兩數相乘，積為正”可得：①或 ②．

解①得x＞；解②得x＜﹣3．

∴不等式的解集為x＞或x＜﹣3．

請你仿照上述方法解決下列問題：

（1）求不等式（2x﹣3）（x+1）＜0的解集．

（2）求不等式≥0的解集．

查看答案和解析>>

科目：初中數學 來源： 題型：

【題目】已知直角三角板和直角三角板，，，．

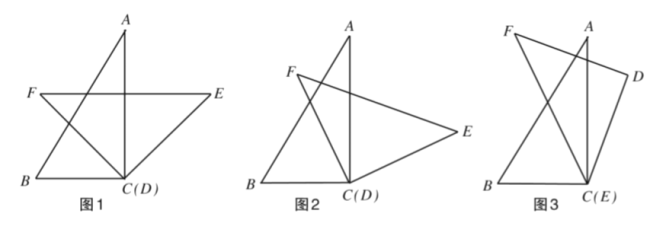
（1）如圖1，將頂點和頂點重合，保持三角板不動，將三角板繞點旋轉，當平分時，求的度數；

（2）在（1）的條件下，繼續旋轉三角板，猜想與有怎樣的數量關系？并利用圖2所給的情形說明理由；

（3）如圖3，將頂點和頂點重合，保持三角板不動，將三角板繞點旋轉．當落在內部時，直接寫出與之間的數量關系．

查看答案和解析>>

科目：初中數學 來源： 題型：

【題目】如圖，已知直線y=﹣x+4與兩坐標軸分別相交于點A，B兩點，點C是線段AB上任意一點，過C分別作CD⊥x軸于點D，CE⊥y軸于點E．雙曲線y=與CD，CE分別交于點P，Q兩點，若四邊形ODCE為正方形，且，則k的值是（ ）

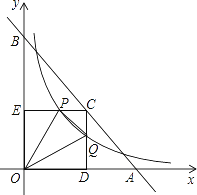
A. 4 B. 2 C. D.

查看答案和解析>>

同步練習冊答案
主站蜘蛛池模板： 精品日韩欧美一区二区在线播放 | 在线免费精品视频 | 中文字幕av在线 | 日韩影院一区 | 黄色你懂的 | 欧美午夜一区二区福利视频 | 欧美一区高清 | 一区二区精品视频 | 国产精品影院在线观看 | 99精品欧美一区二区三区综合在线 | 欧美在线播放一区 | 91精品国产综合久久久久久丝袜 | 欧美亚洲午夜 | 欧美精品一级 | 久久青| 欧美一区二区三区在线观看 | 成人亚洲免费 | 国产亚洲二区 | 日本h视频在线观看 | 国产成人高清视频 | 激情国产 | 99精品播放 | 人人草视频在线观看 | 中文字幕一区二区三区乱码图片 | 91性高湖久久久久久久久_久久99 | 欧美精品在线一区二区三区 | 欧美午夜视频 | 一区二区国产精品 | 亚洲清色| 国产精品免费看 | 日韩激情一区二区 | 亚洲国产日韩在线 | 亚洲精品在线播放视频 | 日韩伦理一区二区三区 | 日韩国产欧美一区 | 亚洲视频一区二区在线 | 国产成人精品久久 | 欧美性猛xxx| 欧美三级欧美成人高清www | 国产一级视频 | 日日干夜夜干 |