
【題目】如圖,直線a∥b,那么∠α的度數是________.

【答案】72°
【解析】
過A作AE∥a,過B作BF∥a,過C作CR∥a,推出直線a∥b∥AE∥BF∥CR,根據平行線的性質推出∠RCT=∠CTZ=30°,求出∠RCB=∠CBF=18°,求出∠ABF=12°=∠EAB,進一步求出∠YWA=180°-∠QWY=60°=∠WAE,根據∠α=∠WAE+∠EAB即可求出答案.
過A作AE∥a,過B作BF∥a,過C作CR∥a,
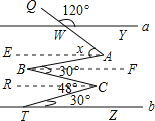
∵直線a∥b,
∴直線a∥b∥AE∥BF∥CR,
∴∠RCT=∠CTZ=30°,
∵∠BCT=48°,
∴∠BCR=48°-30°=18°,
∴∠RCB=∠CBF=18°,
∴∠ABF=30°-18°=12°=∠EAB,
∵∠QWY=120°,
∴∠YWA=180°-∠QWY=60°,
∴∠WAE=∠YWA=60°,
∴∠α=∠WAE+∠EAB=60°+12°=72°,
故答案為:72°.


 名校課堂系列答案
名校課堂系列答案科目:初中數學 來源: 題型:
【題目】如圖,在數軸上點A表示的數a、點B表示數b,a、b滿足|a﹣30|+(b+6)2=0.點O是數軸原點.
![]()
(1)點A表示的數為 ,點B表示的數為 ,線段AB的長為 .
(2)若點A與點C之間的距離表示為AC,點B與點C之間的距離表示為BC,請在數軸上找一點C,使AC=2BC,則點C在數軸上表示的數為 .
(3)現有動點P、Q都從B點出發,點P以每秒1個單位長度的速度向終點A移動;當點P移動到O點時,點Q才從B點出發,并以每秒3個單位長度的速度向右移動,且當點P到達A點時,點Q就停止移動,設點P移動的時間為t秒,問:當t為多少時,P、Q兩點相距4個單位長度?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知四邊形ABCD是平行四邊形,對角線AC、BD交于點O,E是BC的中點,以下說法錯誤的是( )

A. OE=![]() DC B. OA=OC C. ∠BOE=∠OBA D. ∠OBE=∠OCE
DC B. OA=OC C. ∠BOE=∠OBA D. ∠OBE=∠OCE
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】觀察圖,下列說法正確的有( )
①同一平面內,過點A有且只有一條直線AC垂直于直線l;②線段AB,AC,AD中,AC最短,根據是“兩點之間的所有連線中,線段最短”;③線段AB,AC,AD中,AC最短,根據是“直線外一點,與直線上各點連接的所有線段中,垂線段最短”;④線段AC的長是點A到直線l的距離.

A. 1個 B. 2個 C. 3個 D. 4個
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】以圖1(以O為圓心,半徑1 的半圓)作為“基本圖形”,分別經歷如下變換能得到圖2的序號是 (多填或錯填得0分,少填酌情給分)
①只要向右平移1個 單位;
② 先以直線AB為對稱軸進行對稱變換,再向右平移1個單位;
③先繞著O旋轉180°,再向右平移1個單位;
④只要繞著某點旋轉180°.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在一個邊長為a(單位:cm)的正方形ABCD中,點E、M分別是線段AC,CD上的動點,連結DE并延長交正方形的邊于點F,過點M作MN⊥DF于H,交AD于N.
(1)如圖1,當點M與點C重合,求證:DF=MN;
(2)如圖2,假設點M從點C出發,以1cm/s的速度沿CD向點D運動,點E同時從點A出發,以 ![]() cm/s速度沿AC向點C運動,運動時間為t(t>0);
cm/s速度沿AC向點C運動,運動時間為t(t>0);
①判斷命題“當點F是邊AB中點時,則點M是邊CD的三等分點”的真假,并說明理由.
②連結FM、FN,△MNF能否為等腰三角形?若能,請寫出a,t之間的關系;若不能,請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在△ABC中,∠ABC=90°,BD為AC的中線,過點C作CE⊥BD于點E,過點A作BD的平行線,交CE的延長線于點F,在AF的延長線上截取FG=BD,連接BG、DF.若AG=13,CF=6,則四邊形BDFG的周長為 . 
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,AB是⊙O的直徑,∠B=∠CAD. 
(1)求證:AC是⊙O的切線;
(2)若點E是 ![]() 的中點,連接AE交BC于點F,當BD=5,CD=4時,求AF的值.
的中點,連接AE交BC于點F,當BD=5,CD=4時,求AF的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在等邊△ABC中,AB=3,D、E分別是AB、AC上的點,且DE∥BC,將△ADE沿DE翻折,與梯形BCED重疊的部分記作圖形L.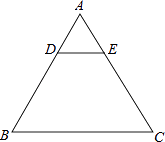
(1)求△ABC的面積;
(2)設AD=x,圖形L的面積為y,求y關于x的函數解析式;
(3)已知圖形L的頂點均在⊙O上,當圖形L的面積最大時,求⊙O的面積.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com