
【題目】(1)(觀察發現)如圖 1,△ABC 和△CDE 都是等邊三角形,且點 B、C、E 在一條直線上,連接 BD 和AE,BD、AE 相交于點 P,則線段 BD 與 AE 的數量關系是 ,BD 與 AE 相交構成的銳角的度數是 .(只要求寫出結論,不必說明理由)

(2)(深入探究 1)如圖 2,△ABC 和△CDE 都是等邊三角形,連接 BD 和 AE,BD、AE 相交于點 P,猜想線段 BD 與 AE 的數量關系,以及 BD 與 AE 相交構成的銳角的度數. 請說明理由 結論:
理由:_______________________

(3)(深入探究 2)如圖 3,△ABC 和△CDE 都是等腰直角三角形,且∠ACB=∠DCE=90°,連接 AD、BE,Q 為 AD 中點,連接 QC 并延長交 BE 于 K. 求證:QK⊥BE.

【答案】(1)BD=AE,60°;
(2)BD=AE,60°;
(3)證明見詳解.
【解析】
(1)根據等邊三角形的性質可得AB=AC,CD=CE,∠ACB=∠DCE=60°,然后求出∠ACE=∠BCD,再利用“邊角邊”證明△ACE和△BCD全等,根據全等三角形對應邊相等可得BD=AE,根據全等三角形對應角相等可得∠AEC=∠BDC,然后根據三角形的一個外角等于與它不相鄰的兩個內角的和求出∠DPE=∠DCE;
(2)根據等邊三角形的性質可得AB=AC,CD=CE,∠ACB=∠DCE=60°,然后求出∠ACE=∠BCD,再利用“邊角邊”證明△ACE和△BCD全等,根據全等三角形對應邊相等可得BD=AE,根據全等三角形對應角相等可得∠AEC=∠BDC,然后根據三角形的內角和定理求出∠DPE=∠DEC;
(3)延長CQ到R,使得CQ=QR,連接AR、DR.只要證明△ACR≌△BCE,可得∠ACR=∠CBE,由∠ACR+∠BCK=90°,推出∠CBE+∠BCK=90°,可得∠CKB=90°,即CK⊥BE.
解:(1)∵△ABC和△CDE都是等邊三角形,
∴AB=AC,CD=CE,∠ACB=∠DCE=60°,
∴∠ACB+∠ACD=∠DCE+∠ACD,
即∠ACE=∠BCD,
在△ACE和△BCD中,
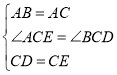 ,
,
∴△ACE≌△BCD(SAS),
∴BD=AE,∠AEC=∠BDC,
由三角形的外角性質,∠DPE=∠AEC+∠DBC,
∠DCE=∠BDC+∠DBC,
∴∠DPE=∠DCE=60°;
(2)結論BD=AE,∠DPE=60°還成立.
∵△ABC和△CDE都是等邊三角形,
∴AB=AC,CD=CE,∠ACB=∠DCE=60°,
∴∠ACB+∠ACD=∠DCE+∠ACD,
即∠ACE=∠BCD,
在△ACE和△BCD中,
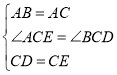 ,
,
∴△ACE≌△BCD(SAS),
∴BD=AE,∠AEC=∠BDC,
∵∠BDC+∠CDE+∠AED
=∠AEC+∠CDE+∠AED
=∠CDE+∠CED
=180°-∠DCE
=180°-60°=120°,
∴∠DPE=180°-(∠BDC+∠CDE+∠AED)=180°-120°=60°;
(3)如圖3中,延長CQ到F,使得CQ=QF,連接AF、DF.
∵△ABC和△CDE都是等腰直角三角形,
∴∠ACB=∠DCE=90°,AC=BC,CE=CD,
∴∠BCE+∠ACD=180°,
∵Q 為 AD 中點,
∴AQ=DQ,
∵CQ=QF,
∴四邊形ACDF是平行四邊形,
∴AF=CD=CE,AF∥CD,
∴∠CAF+∠ACD=180°,
∴∠BCE=∠CAF,∵CA=CB,AF=CE,
∴△ACF≌△BCE,
∴∠ACF=∠CBE,
∵∠ACF+∠BCK=180°-∠ACB =180°-90°=90°,
∴∠CBE+∠BCK=90°,
∴∠CKB=90°,即CK⊥BE.


科目:初中數學 來源: 題型:
【題目】如圖,在△ABC與△DBC中,∠ACB=∠DBC=90°,E是BC的中點,EF⊥AB,AB=DE.
(1)求證:BC=DB;
(2)若BD=8cm,求AC的長.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某市出租車計費辦法如圖所示.根據圖象信息,下列說法錯誤的是( )

A. 出租車起步價是10元
B. 在3千米內只收起步價
C. 超過3千米部分(x>3)每千米收3元
D. 超過3千米時(x>3)所需費用y與x之間的函數關系式是y=2x+4
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在△ABC中,∠ACB=90°,AC=4,BC=3,D是邊AC的中點,CE⊥BD交AB于點E.
(1)求tan∠ACE的值;
(2)求AE:EB.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,長為 ![]() ,寬為
,寬為 ![]() 的大長方形被分割為
的大長方形被分割為 ![]() 小塊,除陰影
小塊,除陰影 ![]() ,
,![]() 外,其余
外,其余 ![]() 塊是形狀、大小完全相同的小長方形,其較短一邊長為
塊是形狀、大小完全相同的小長方形,其較短一邊長為 ![]() .
.

(1)每個小長方形較長的一邊長是 ![]() (用含
(用含 ![]() 的代數式表示).
的代數式表示).
(2)分別用含 ![]() ,
,![]() 的代數式表示陰影
的代數式表示陰影 ![]() ,
,![]() 的面積,并計算陰影 A 的面積與陰影B的面積的差.
的面積,并計算陰影 A 的面積與陰影B的面積的差.
(3)當 ![]() 時,陰影
時,陰影 ![]() 與陰影
與陰影 ![]() 的面積差會隨著
的面積差會隨著 ![]() 的變化而變化嗎?請你作出判斷,并說明理由.
的變化而變化嗎?請你作出判斷,并說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】用圖1中四個完全一樣的直角三角形可以拼成圖2的大正方形。

解答下列問題:
(1)請用含![]() 、
、![]() 、
、![]() 的代數式表示大正方形的面積.
的代數式表示大正方形的面積.
方法1: ;方法2: .
(2)根據圖2,利用圖形的面積關系,推導![]() 、
、![]() 、
、![]() 之間滿足的關系式.
之間滿足的關系式.
(3)利用(2)的關系式解答:如果大正方形的面積是25,且![]() ,求小正方形的面積.
,求小正方形的面積.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,△ABC內接于⊙O,BD為⊙O的直徑,BD與AC相交于點H,AC的延長線與過點B的直線相交于點E,且∠A=∠EBC.

(1)求證:BE是⊙O的切線;
(2)已知CG∥EB,且CG與BD、BA分別相交于點F、G,若BGBA=48,FG=![]() ,DF=2BF,求AH的值.
,DF=2BF,求AH的值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com