
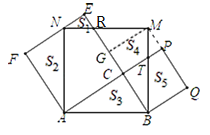
【題目】如圖,以AB為斜邊的Rt△ABC的每條邊為邊作三個正方形,分別是正方形ABMN,正方形BCPQ,正方形ACEF,且邊EF恰好經過點N.若S3=S4=6,則S1+S5=_____.(注:圖中所示面積S表示相應封閉區域的面積,如S3表示△ABC的面積)

【答案】6
【解析】
如圖,連接MQ,作MG⊥EC于G,設PC交BM于T,MN交EC于R.先證明△ABC≌△MBQ(SAS),推出∠ACB=∠BQM=90°,由∠PQB=90°,推出M,P,Q共線,由四邊形CGMP是矩形,推出MG=PC=BC,證明△MGR≌△BCT(AAS),推出MR=BT,由MN=BM,NR=MT,可證△NRE≌MTP,推出S1+S5=S3=6.
如圖,連接MQ,作MG⊥EC于G,設PC交BM于TMN交EC于R.
∵∠ABM=∠CBQ=90°,
∴∠ABC=∠MBQ,
∵BA=BM,BC=BQ,
在△ABC和△MBQ,
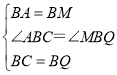 ,
,
∴△ABC≌△MBQ(SAS),
∴∠ACB=∠BQM=90°,
∵∠PQB=90°,
∴M,P,Q共線,
∵四邊形CGMP是矩形,
∴MG=PC=BC,
∵∠BCT=∠MGR=90°,∠BTC+∠CBT=90°,∠BRM+∠CBT=90°,
∴∠MRG=∠BTC,
在△MGR和△BCT中
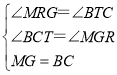 ,
,
∴△MGR≌△BCT(AAS),
∴MR=BT,![]()
又∵MN=BM,![]()
∴NR=MT,![]() ,
,
在△NRE和MTP,
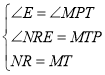
∴△NRE≌MTP(AAS),
∴S1+S5=S3=6,
故答案是:6.


 天天練口算系列答案
天天練口算系列答案科目:初中數學 來源: 題型:
【題目】某廠家新開發的一種摩托車如圖所示,它的大燈![]() 射出的光線
射出的光線![]() 、
、![]() 與地面
與地面![]() 的夾角分別為
的夾角分別為![]() 和
和![]() ,大燈
,大燈![]() 離地面距離
離地面距離![]() .
.
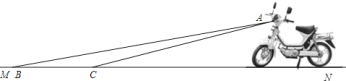
![]() 該車大燈照亮地面的寬度
該車大燈照亮地面的寬度![]() 約是多少(不考慮其它因素)?
約是多少(不考慮其它因素)?
![]() 一般正常人從發現危險到做出剎車動作的反應時間是
一般正常人從發現危險到做出剎車動作的反應時間是![]() ,從發現危險到摩托車完全停下所行駛的距離叫做最小安全距離,某人以
,從發現危險到摩托車完全停下所行駛的距離叫做最小安全距離,某人以![]() 的速度駕駛該車,從
的速度駕駛該車,從![]() 到摩托車停止的剎車距離是
到摩托車停止的剎車距離是![]() ,請判斷該車大燈的設計是否能滿足最小安全距離的要求,請說明理由.(參考數據:
,請判斷該車大燈的設計是否能滿足最小安全距離的要求,請說明理由.(參考數據:![]() ,
,![]() ,
,![]() ,
,![]() )
)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】(1)操作發現:
在△ABC中,AB=AC,∠BAC=90°,D在線段BC上(不與點B重合),連接AD,將線段AD繞A點逆時針旋轉90°得到AE,連接EC,如圖①所示,請直接寫出線段CE和BD的位置關系和數量關系.
(2)猜想論證:
在(1)的條件下,當D在線段BC的延長線上時,請你在圖②中畫出圖形并判斷(1)中的結論是否成立,并證明你的判斷.
(3)拓展延伸:
如圖③,若AB≠AC,∠BAC≠90°,點D在線段BC上運動,試探究:當銳角∠ACB等于 度時,線段CE和BD之間的位置關系仍成立(點C、E重合除外)?此時若作DF⊥AD交線段CE于點F,且當AC=3![]() 時,請直接寫出線段CF的長的最大值是 .
時,請直接寫出線段CF的長的最大值是 .

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在![]() 中,
中,![]() ,
,![]() ,
,![]() 分別是
分別是![]() ,
,![]() 上的動點,將
上的動點,將![]() 沿
沿![]() 折疊.
折疊.
(1)當點![]() 與點
與點![]() 重合時,如圖1.若
重合時,如圖1.若![]() ,
,![]() ,則
,則![]() 的周長為_____.
的周長為_____.
(2)定義:若在三角形中,期中一條邊是另一條邊的2倍,則稱這個三角形為“倍邊三角形”.當點![]() 與點
與點![]() 重合時,如圖2.若
重合時,如圖2.若![]() ,則
,則![]() 是倍邊三角形嗎?請說明理由.
是倍邊三角形嗎?請說明理由.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知拋物線y=ax2+bx+3過等腰Rt△BOC的兩頂點B、C,且與x軸交于點A(﹣1,0).
(1)求拋物線的解析式;
(2)拋物線的對稱軸與直線BC相交于點M,點N為x軸上一點,當以M,N,B為頂點的三角形與△ABC相似時,求BN的長度;
(3)P為線段BC上方的拋物線上的一個動點,P到直線BC的距離是否存在最大值?若存在,請求出這個最大值的大小以及此時點P的坐標;若不存在,請說明理由.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】設y是關于x的一次函數,其圖象與y軸交點的縱坐標為﹣10,且當x=1時,y=﹣5.
(1)求該一次函數圖象與坐標軸圍成的三角形面積;
(2)當函數值為![]() 時,自變量的取值是多少?
時,自變量的取值是多少?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在平面直角坐標系中,點A在y軸上,其坐標為(0,4),x軸上的一動
P從原點O出發,沿x軸正半軸方向運動,速度為每秒1個單位長度,以P為直角頂點
第一象限內作等腰Rt△APB.設P點的運動時間為t秒.

(1)填空:當t=2時,點B的坐標為.
(2)在P點的運動過程中,當AB∥x軸時,求t的值;
(3)通過探索,發現無論P點運動到何處,點B始終在一直線上,試求出該直線的函數解析式.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在Rt△ABC中,∠BAC=90°,AD⊥BC于D,將AB邊沿AD折疊,發現B點的對應點E正好在AC的垂直平分線上,則∠C=_______
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com