
【題目】閱讀:
我們知道,![]() 于是要解不等式
于是要解不等式![]() ,我們可以分兩種情況去掉絕對值符號,轉化為我們熟悉的不等式,按上述思路,我們有以下解法:
,我們可以分兩種情況去掉絕對值符號,轉化為我們熟悉的不等式,按上述思路,我們有以下解法:
解:(1)當![]() ,即
,即![]() 時:
時:![]()
解這個不等式,得:![]()
由條件![]() ,有:
,有:![]()
(2)當![]() ,即
,即![]() 時,
時,![]()
解這個不等式,得:![]()
由條件![]() ,有:
,有:![]()
∴ 如圖,![]()
綜合(1)、(2)原不等式的解為:![]()
根據以上思想,請探究完成下列![]() 個小題:
個小題:
![]() ;
;
![]()
 智能訓練練測考系列答案
智能訓練練測考系列答案科目:初中數學 來源: 題型:
【題目】如圖,在3×3的方格中,A,B,C,D,E,F分別位于格點上,從C,D,E,F四點中任意取一點,與點A,B為頂點作三角形,則所作三角形為等腰三角形的概率是( )
A.1
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,D是△ABC內一點,BD⊥CD,AD=6,BD=4,CD=3,E,F,G,H分別是AB,AC,CD,BD的中點,則四邊形EFGH的周長是( )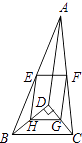
A.7
B.9
C.10
D.11
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】2016年國際馬拉松賽于承德市舉辦,起點承德市獅子園,賽道為外環路,終點為奧體中心(賽道基本為直線).在賽道上有A,B兩個服務點,現有甲,乙兩個服務人員,分別從A,B兩個服務點同時出發,沿直線勻速跑向終點C(奧體中心),如圖1所示,設甲、乙兩人出發xh后,與B點的距離分別為y甲km、y乙km,y甲、y乙與x的函數關系如圖2所示.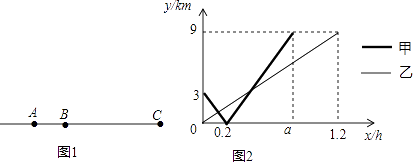
(1)從服務點A到終點C的距離為km,a=h;
(2)求甲乙相遇時x的值;
(3)甲乙兩人之間的距離應不超過1km時,稱為最佳服務距離,從甲、乙相遇到甲到達終點以前,保持最佳服務距離的時間有多長?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某中學改革學生的學習模式,變“老師要學生學習”為“學生自主學習”,培養了學生自主學習的能力.小華與小明同學就“你最喜歡哪種學習方式”隨機調查了他們周圍的一些同學,根據收集到的數據繪制了以下兩個不完整的統計圖(如圖).
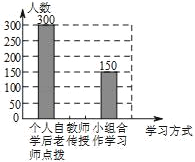
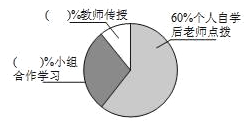
請根據上面兩個不完整的統計圖回答以下4個問題:
(1)這次抽樣調查中,共調查了_____名學生.
(2)補全條形統計圖中的缺項.
(3)在扇形統計圖中,選擇教師傳授的占_____%,選擇小組合作學習的占_____%.
(4)根據調查結果,估算該校1800名學生中大約有_____人選擇小組合作學習模式.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在平面直角坐標系中,O為坐標原點,A(1,3),B(2,1),直角坐標系中存在點C,使得O,A,B,C四點構成平行四邊形,則C點的坐標為______________________________.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】下列敘述中:![]() 任意一個三角形的三條高至少有一條在此三角形內部;
任意一個三角形的三條高至少有一條在此三角形內部;![]() 以a,b,c為邊
以a,b,c為邊![]() b,c都大于0,且
b,c都大于0,且![]() 可以構成一個三角形;
可以構成一個三角形;![]() 一個三角形內角之比為3:2:1,此三角形為直角三角形;
一個三角形內角之比為3:2:1,此三角形為直角三角形;![]() 有兩個角和一條邊對應相等的兩個三角形全等;正確的有
有兩個角和一條邊對應相等的兩個三角形全等;正確的有![]()
![]() 個.
個.
A. 1B. 2C. 3D. 4
查看答案和解析>>
科目:初中數學 來源: 題型:
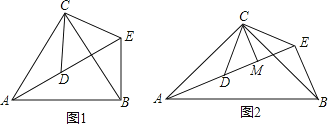
【題目】已知:如圖1,![]() 和
和![]() 均為等邊三角形,點A、D、E在同一直線上,連接BE.
均為等邊三角形,點A、D、E在同一直線上,連接BE.
![]() 求證:
求證:![]() ;
;
![]() 求
求![]() 的度數;
的度數;
![]() 拓展探究:如圖2,
拓展探究:如圖2,![]() 和
和![]() 均為等腰直角三角形,
均為等腰直角三角形,![]() ,點A、D、E在同一直線上,CM為
,點A、D、E在同一直線上,CM為![]() 中DE邊上的高,連接BE.
中DE邊上的高,連接BE.
![]() 的度數為______
的度數為______![]() ;
;![]() 探索線段CM、AE、BE之間的數量關系為______
探索線段CM、AE、BE之間的數量關系為______![]() 直接寫出答案,不需要說明理由
直接寫出答案,不需要說明理由![]() .
.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知關于x的方程x2+ax+a﹣2=0
(1)若該方程的一個根為1,求a的值及該方程的另一根;
(2)求證:不論a取何實數,該方程總有兩個不相等的實數根
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com