圓外切等腰梯形一腰長為5cm，則梯形的中位線長為（ ）
A．10cm
B．5cm
C．20cm
D．15cm
【答案】
分析：根據切線長定理得出AE=AF，DE=DH，CG=CH，BG=BF，求出AD+BC=AB+CD=10cm，根據梯形的中位線定理求出即可．
解答：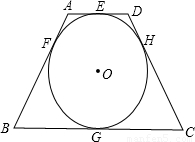
解：∵⊙O的外切等腰梯形ABCD，切點分別為E、F、G、H，
∴由切線長定理得：AE=AF，DE=DH，CG=CH，BG=BF，
∴AE+DE+BG+CG=AF+DH+BF+CH，
即AD+BC=AB+CD=5cm+5cm=10cm，
∴由梯形的中位線定理得：梯形的中位線為
（AD+BC）=5cm，
故選B．
點評：本題考查了等腰梯形性質，梯形的中位線定理，切線長定理等知識點，關鍵是求出AD+BC的長．
黃岡冠軍課課練系列答案
