
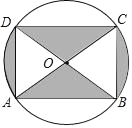
【題目】如圖是某商品的標志圖案,AC與BD是⊙O的兩條直徑,首尾順次連接點A、B、C、D,得到四邊形ABCD,若AC=10cm,∠BAC=36°,則圖中陰影部分的面積為_____.
【答案】10πcm2.
【解析】分析:根據已知條件得到四邊形ABCD是矩形,求得圖中陰影部分的面積=S扇形AOD+S扇形BOC=2S扇形AOD,根據等腰三角形的性質得到∠BAC=∠ABO=36°,由圓周角定理得到∠AOD=72°,于是得到結論.
詳解:∵AC與BD是⊙O的兩條直徑,
∴∠ABC=∠ADC=∠DAB=∠BCD=90°,
∴四邊形ABCD是矩形,
∴S△ABO=S△CDO =S△AOD=S△BOD,
∴圖中陰影部分的面積=S扇形AOD+S扇形BOC=2S扇形AOD,
∵OA=OB,
∴∠BAC=∠ABO=36°,
∴∠AOD=72°,
∴圖中陰影部分的面積=2×![]() =10π,
=10π,
故答案為:10πcm2.


科目:初中數學 來源: 題型:
【題目】如圖,在![]() ABCD中,點E為CD的中點,點F在BC上,且CF=2BF,連接AE,AF,若AF=
ABCD中,點E為CD的中點,點F在BC上,且CF=2BF,連接AE,AF,若AF=![]() ,AE=7,tan∠EAF=
,AE=7,tan∠EAF=![]() ,則線段BF的長為__________.
,則線段BF的長為__________.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某檢修小組從A地出發,在東西方向的馬路上檢修線路,如果規定向東行駛為正,向西行駛為負,一天中七次行駛紀錄如下.(單位:km)
第一次 | 第二次 | 第三次 | 第四次 | 第五次 | 第六次 | 第七次 |
-4 | +8 | -9 | +8 | +6 | -5 | -2 |
(1)求收工時距A地多遠?
(2)若每km耗油0.4升,問一天共耗油多少升?
查看答案和解析>>
科目:初中數學 來源: 題型:
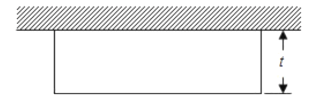
【題目】有長為l的籬笆,利用它和房屋的一面墻圍成如圖形狀的園子,園子的寬為t.
(1)用關于l,t的代數式表示園子的面積;這個代數式是多項式還是單項式?
(2)若l=100固定不變,若t的值取20,25,30時,則哪一種取法所圍成的園子面積最大?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在平面直角坐標系中,一次函數![]() 的圖像與反比例函數
的圖像與反比例函數![]() 的圖像交于第一、三象限內的
的圖像交于第一、三象限內的![]() 、
、![]() 兩點,與
兩點,與![]() 軸交于點
軸交于點![]() ,點
,點![]() 在
在![]() 軸負半軸上,
軸負半軸上,![]() ,且四邊形
,且四邊形![]() 是平行四邊形,點
是平行四邊形,點![]() 的縱坐標為
的縱坐標為![]() .
.
(1)求該反比例函數和一次函數的表達式;
(2)連接![]() ,求
,求![]() 的面積;
的面積;
(3)直接寫出關于![]() 的不等式
的不等式![]() 的解集.
的解集.

查看答案和解析>>
科目:初中數學 來源: 題型:
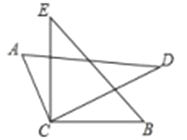
【題目】將一副三角板中的兩塊如圖所示的方式疊放在一起,直角頂點重合.
(1)若![]() 時,求
時,求![]() 的度數;
的度數;
(2)當![]() 平分
平分![]() 時,求
時,求![]() 的度數(請寫出計算過程);
的度數(請寫出計算過程);
(3)猜想并直接寫出![]() 與
與![]() 的數量關系(不必說明理由).
的數量關系(不必說明理由).
查看答案和解析>>
科目:初中數學 來源: 題型:
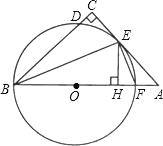
【題目】如圖,在△ABC中,∠C=90°,∠ABC的平分線交AC于點E,過點E作BE的垂線交AB于點F,⊙O是△BEF的外接圓.
(1)求證:AC是⊙O的切線;
(2)過點E作EH⊥AB,垂足為H,求證:CD=HF;
(3)若CD=1,EH=3,求BF及AF長.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】閱讀理解:若A、B、C為數軸上三點,若點C到A的距離是點C到B的距離2倍,我們就稱點C是(A,B)的好點.
例如,如圖1,點A表示的數為-1,點B表示的數為2.表示1的點C到點A的距離是2,到點B的距離是1,那么點C是(A,B)的好點;
又如,表示0的點D到點A的距離是1,到點B的距離是2,那么點D就不是(A,B)的好點,但點D是(B,A)的好點.
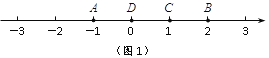
知識運用:
⑴ 如圖1,點B是(D,C)的好點嗎? (填是或不是);
⑵ 如圖2,A、B為數軸上兩點,點A所表示的數為-40,點B所表示的數為20.現有一只電子螞蟻P從點B出發,以2個單位每秒的速度向左運動,到達點A停止.當t為何值時,P、A和B中恰有一個點為其余兩點的好點?

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com