
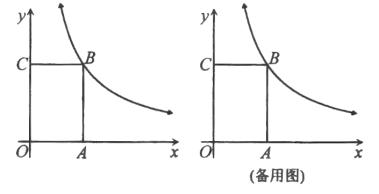
【題目】如圖,矩形![]() 的頂點
的頂點![]() 分別在
分別在![]() 軸的正半軸上,點
軸的正半軸上,點![]() 在反比例函數
在反比例函數![]() 的第一象限內的圖像上,
的第一象限內的圖像上,![]() ,動點
,動點![]() 在
在![]() 軸的上方,且滿足
軸的上方,且滿足![]() .
.
(1)若點![]() 在這個反比例函數的圖像上,求點
在這個反比例函數的圖像上,求點![]() 的坐標;
的坐標;
(2)連接![]() ,求
,求![]() 的最小值;
的最小值;
(3)若點![]() 是平面內一點,使得以
是平面內一點,使得以![]() 為頂點的四邊形是菱形,則請你直接寫出滿足條件的所有點
為頂點的四邊形是菱形,則請你直接寫出滿足條件的所有點![]() 的坐標.
的坐標.
【答案】(1)點P的坐標為(6,2);(2)![]() ;(3)Q
;(3)Q![]() (4
(4![]() ,5),Q
,5),Q![]() (4+
(4+![]() ,5),Q
,5),Q![]() (42
(42![]() ,1),Q
,1),Q![]() (4+2
(4+2![]() ,1).
,1).
【解析】
(1)首先根據點B坐標,確定反比例函數的解析式,設點P的縱坐標為m(m>0),根據![]() ,構建方程即可解決問題;
,構建方程即可解決問題;
(2)過點(0,2),作直線l⊥y軸,由(1)知,點P的縱坐標為2,推出點P在直線l上作點O關于直線l的對稱點O',則OO'=4,連接AO'交直線l于點P,此時PO+PA的值最小;
(3)分兩種情形分別求解即可解決問題;
(1)∵四邊形OABC是矩形,OA=4,OC=3,
∴點B的坐標為(4,3),
∵點B在反比例函數![]() 的第一象限內的圖象上
的第一象限內的圖象上
∴k=12,
∴y=![]() ,
,
設點P的縱坐標為m(m>0),
∵![]() .
.
∴![]() OAm=OAOC
OAm=OAOC![]() ,
,
∴m=2,
當點,P在這個反比例函數圖象上時,則2=![]() ,
,
∴x=6
∴點P的坐標為(6,2).
(2)過點(0,2),作直線l⊥y軸.

由(1)知,點P的縱坐標為2,
∴點P在直線l上
作點O關于直線l的對稱點O',則OO'=4,
連接AO'交直線l于點P,此時PO+PA的值最小,
則PO+PA的最小值=PO'+PA=O'A=![]() .
.
(3)

①如圖2中,當四邊形ABQP是菱形時,易知AB=AP=PQ=BQ=3,P![]() (4
(4![]() ,2),P
,2),P![]() (4
(4![]() ,2),
,2),
∴Q![]() (4
(4![]() ,5),Q
,5),Q![]() (4+
(4+![]() ,5).
,5).
②如圖3中,當四邊形ABPQ是菱形時,P![]() (42
(42![]() ,2),P
,2),P![]() (4+2
(4+2![]() ,2),
,2),
∴Q![]() (42
(42![]() ,1),Q
,1),Q![]() (4+2
(4+2![]() ,1).
,1).
綜上所述,點Q的坐標為Q![]() (4
(4![]() ,5),Q
,5),Q![]() (4+
(4+![]() ,5),Q
,5),Q![]() (42
(42![]() ,1),Q
,1),Q![]() (4+2
(4+2![]() ,1).
,1).


科目:初中數學 來源: 題型:
【題目】我國明代數學家程大位在他六十歲時終于完成了《外法統宗》的編撰.這是- -木簡明實用的數學書,書中列出了許多應用題的數字計算
請從![]() 兩題中任選-題做答.
兩題中任選-題做答.
![]() :有一群人分銀子,如果每人分七兩,則剩余四兩;如果每人分九兩,則還差半斤,設所分銀子共
:有一群人分銀子,如果每人分七兩,則剩余四兩;如果每人分九兩,則還差半斤,設所分銀子共![]() 兩.根據題意列出的方程是____________ .( 注:明代時
兩.根據題意列出的方程是____________ .( 注:明代時![]() 兩.故有“半斤八兩”這個成語)
兩.故有“半斤八兩”這個成語)
![]() :用九百九十九文錢共買了一千個甜果和苦果.其中四文錢可以買甜果七個,十一文錢可以買苦果九個,設買了
:用九百九十九文錢共買了一千個甜果和苦果.其中四文錢可以買甜果七個,十一文錢可以買苦果九個,設買了![]() 個甜果,根據題意列出的方程是__________.
個甜果,根據題意列出的方程是__________.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】2018年4月8日—11日,博鰲亞洲論壇2018年年會在海南省博鰲鎮召開.本屆博鰲亞洲論壇的主題為“開放創新的亞洲,繁榮發展的世界”.圍繞這一主題,年會設置了“全球化與一帶一路”“開放的亞洲”“創新”“改革再出發”四大板塊,展開60多場正式討論.某廠準備生產甲、乙兩種商品共8萬件銷往“一帶一路”沿線國家和地區,已知2件甲種商品與3件乙種商品的銷售收入相同,3件甲種商品比2件乙種商品的銷售收入多1500元.
(1)甲種商品與乙種商品的銷售單價各多少元?
(2)若甲、乙兩種商品的銷售總收入不低于5400萬元,則至少銷售甲種商品多少萬件?
查看答案和解析>>
科目:初中數學 來源: 題型:
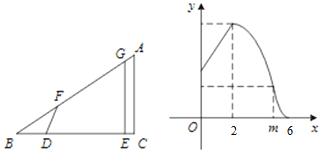
【題目】如圖 , ![]() 中,
中, ![]() ,線段
,線段![]() 在射線
在射線![]() 上,且
上,且![]() ,線段
,線段![]() 沿射線
沿射線![]() 運動,開始時,點
運動,開始時,點![]() 與點
與點![]() 重合,點
重合,點![]() 到達點
到達點![]() 時運動停止,過點
時運動停止,過點![]() 作
作![]() ,與射線
,與射線![]() 相交于點
相交于點![]() ,過點
,過點![]() 作
作![]() 的垂線,與射線
的垂線,與射線![]() 相交于點
相交于點![]() .設
.設![]() ,四邊形
,四邊形![]() 與
與![]() 重疊部分的面積為
重疊部分的面積為![]() 關于
關于![]() 的函數圖象如圖所示(其中
的函數圖象如圖所示(其中![]() 時,函數的解析式不同)
時,函數的解析式不同)
(1)填空: ![]() 的長是 ;
的長是 ;
(2)求![]() 關于
關于![]()
![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某市某校推進新課改的過程中,開設的體育選修課有:![]() :籃球,
:籃球,![]() :足球,
:足球,![]() :排球,
:排球,![]() :羽毛球,
:羽毛球,![]() :乒乓球,學生可根據自己的愛好選修一門,學校李老師對某班全班同學的選課情況進行調查統計,制成了兩幅不完整的統計圖(如圖).
:乒乓球,學生可根據自己的愛好選修一門,學校李老師對某班全班同學的選課情況進行調查統計,制成了兩幅不完整的統計圖(如圖).

(1)該班學生人數是________,并補全頻數分布直方圖;
(2)表示“羽毛球”所在扇形的圓心角是________;
(3)若該校共有學生3500名,請估計有多少人選修足球?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】對x,y定義一種新運算T,規定:T(x,y)=![]() (其中a、b均為非零常數),這里等式右邊是通常的四則運算,例如:T(0,1)=
(其中a、b均為非零常數),這里等式右邊是通常的四則運算,例如:T(0,1)=![]() =b.
=b.
(1)已知T(1,﹣1)=﹣2,T(4,2)=1.
①求a,b的值;
②若關于m的不等式組![]() 恰好有3個整數解,求實數p的取值范圍;
恰好有3個整數解,求實數p的取值范圍;
(2)若T(x,y)=T(y,x)對任意實數x,y都成立(這里T(x,y)和T(y,x)均有意義),則a,b應滿足怎樣的關系式?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知:如圖,折疊矩形ABCD,使點B落在對角線AC上的點F處,若BC=8,AB=6,則線段CE的長度是( )

A. 3 B. 4 C. 5 D. 6
查看答案和解析>>
科目:初中數學 來源: 題型:
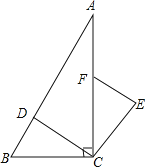
【題目】如圖,在Rt△ABC中,∠ACB=90°,點D,F分別在AB,AC上,CF=CB.連接CD,將線段CD繞點C按順時針方向旋轉90°后得CE,連接EF.
(1)求證:△BCD≌△FCE;
(2)若EF∥CD.求∠BDC的度數.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com