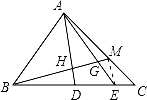
如圖，△ABC中，D、E是BC邊上的點，BD：DE：EC=3：2：1，M在AC邊上，CM：MA=1：2，BM交AD，AE于H，G，則BH：HG：GM等于（ ）
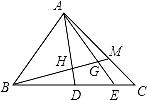
A．3：2：1 B．5：3：1 C．25：12：5 D．51：24：10
D【考點】相似三角形的判定與性質．
【專題】計算題．
【分析】連接EM，根據已知可得△BHD∽△BME，△CEM∽△CDA，根據相似比從而不難得到答案．
【解答】解：連接EM，
CE：CD=CM：CA=1：3
∴EM平行于AD
∴△BHD∽△BME，△CEM∽△CDA
∴HD：ME=BD：BE=3：5，ME：AD=CM：AC=1：3
∴AH
=（3﹣
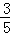）ME，
∴AH：ME=12：5
∴HG：GM=AH：EM=12：5
設GM=5k，GH=12k，
∵BH：HM=3：2=BH：17k
∴BH=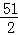
K，
∴BH：HG：GM=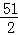k：12k：5k=51：24：10
故選D．
【點評】此題主要考查相似三角形的性質的理解及運用．
津橋教育計算小狀元系列答案科目：初中數學 來源： 題型：
二次函數y=ax2+bx+c的圖象如圖所示，則下列結論中錯誤的是（ ）
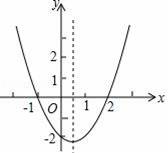
A．函數有最小值 B．當﹣1＜x＜2時，y＞0
C．a+b+c＜0 D．當x＜
，y隨x的增大而減小
查看答案和解析>>
科目：初中數學 來源： 題型：
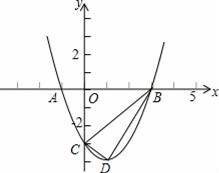
如圖，已知拋物線y=ax2+bx﹣3與x軸的一個交點為A（﹣1，0），另一個交點為B，與y軸的交點為C，其頂點為D，對稱軸為直線x=1．
（1）求拋物線的解析式；
（2）已知點M為y軸上的一個動點，當△ACM是以AC為一腰的等腰三角形時，求點M的坐標．
查看答案和解析>>
科目：初中數學 來源： 題型：
將拋物線y=﹣2x2+1向右平移1個單位，再向下平移3個單位后所得到的拋物線為（ ）
A．y=﹣2（x+1）2﹣2 B．y=﹣2（x+1）2﹣4 C．y=﹣2（x﹣1）2﹣2 D．y=﹣2（x﹣1）2﹣4
查看答案和解析>>
科目：初中數學 來源： 題型：
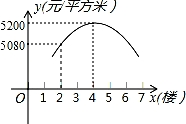
某市新建成的一批樓房都是8層，房子的價格y（元/平方米）隨樓層數x（樓）的變化而變化．已知點（x，y）都在一個二次函數的圖象上（如圖），則6樓房子的價格為 元/平方米．
查看答案和解析>>
科目：初中數學 來源： 題型：
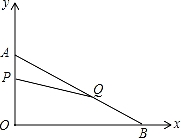
在平面直角坐標系內，已知點A（0，6），點B（8，0），動點P從點A開始在線段AO上以每秒1個單位長度的速度向點O移動，同時動點Q從點B開始在線段BA上以每秒2個單位長度的速度向點A移動，設點P、Q移動的時間為t秒．
（1）求直線AB的解析式；
（2）當t=2秒時，求四邊形OPQB的面積；
（3）當t為何值時，以點A、P、Q為頂點的三角形與△AOB相似？
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
CE，求線段CE的長．
有意義，那么x的取值范圍是__________