
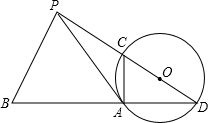
 A、C,連PA,若∠PAC=∠D.
A、C,連PA,若∠PAC=∠D.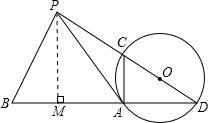
 x,
x, =
= a,
a,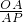 =
=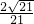 .
. x,又由于∠CAD=∠PMD=90°,根據同位角相等,兩直線平行,可得AC∥PM,因此有CD:DP=DA:DM=4:7,若CD=4a,DP=7a,那么OA=OC=2a,CP=3a,則OP=5a,利用勾股定理可求AP=
x,又由于∠CAD=∠PMD=90°,根據同位角相等,兩直線平行,可得AC∥PM,因此有CD:DP=DA:DM=4:7,若CD=4a,DP=7a,那么OA=OC=2a,CP=3a,則OP=5a,利用勾股定理可求AP= a,從而易求tan∠APC=
a,從而易求tan∠APC=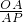 =
=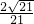 .
.

 各地期末復習特訓卷系列答案
各地期末復習特訓卷系列答案 小博士期末闖關100分系列答案
小博士期末闖關100分系列答案科目:初中數學 來源: 題型:
| 1 | 2 |
 使△PBD的周長最小?若存在,求出點P的坐標;若不存在,請說明理由.
使△PBD的周長最小?若存在,求出點P的坐標;若不存在,請說明理由.查看答案和解析>>
科目:初中數學 來源: 題型:
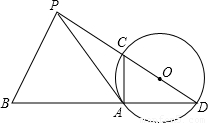
 A、C,連PA,若∠PAC=∠D.
A、C,連PA,若∠PAC=∠D.查看答案和解析>>
科目:初中數學 來源:2010年湖北省武漢市中考數學模擬試卷(22)(解析版) 題型:解答題

查看答案和解析>>
科目:初中數學 來源:2010年湖北省武漢市中考數學模擬試卷(10)(解析版) 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com