
【題目】如圖1,點![]() 是線段
是線段![]() 上的動點(點
上的動點(點![]() 與
與![]() 不重合),分別以
不重合),分別以![]() 為邊向線段
為邊向線段![]() 的同一側作正
的同一側作正![]() 和正
和正![]() .
.
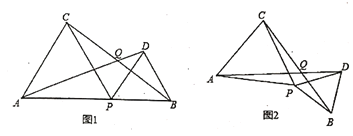
(1)請你判斷![]() 與
與![]() 有怎樣的數量關系?請說明理由;
有怎樣的數量關系?請說明理由;
(2)連接![]() ,相交于點
,相交于點![]() ,設
,設![]() ,那么
,那么![]() 的大小是否會隨點
的大小是否會隨點![]() 的移動而變化?請說明理由;
的移動而變化?請說明理由;
(3)如圖2,若點![]() 固定,將
固定,將![]() 繞點
繞點![]() 按順時針方向旋轉(旋轉角小于
按順時針方向旋轉(旋轉角小于![]() ),此時
),此時![]() 的大小是否發生變化?(只需直接寫出你的猜想,不必證明)
的大小是否發生變化?(只需直接寫出你的猜想,不必證明)
【答案】(1)![]() ,見解析;(2)
,見解析;(2)![]() 的大小不會隨點
的大小不會隨點![]() 的移動而變化,見解析;(3)此時
的移動而變化,見解析;(3)此時![]() 的大小不會發生改變,始終等于
的大小不會發生改變,始終等于![]() .
.
【解析】
(1)先根據SAS證明![]() ≌
≌![]() ,再根據全等三角形的性質即得結論;
,再根據全等三角形的性質即得結論;
(2)如圖3,根據![]() ≌
≌ ![]() 可得
可得![]() ,再在△APF和△CQF中用三角形內角和定理即可證得結論;
,再在△APF和△CQF中用三角形內角和定理即可證得結論;
(3)旋轉的過程中,(2)中的兩個三角形的全等關系不變,因而角度不會變化.
解:(1)![]() .
.
理由如下:
因為![]() 是等邊三角形,
是等邊三角形,
所以![]() ,
,
又因為![]() 是等邊三角形,
是等邊三角形,
所以![]() ,
,
又因為![]() 三點在同一直線上,
三點在同一直線上,
所以![]() .
.
在![]() 和
和![]() 中
中
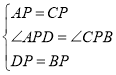
所以![]() ≌
≌ ![]() (SAS).
(SAS).
所以![]() .
.
(2)![]() 的大小不會隨點
的大小不會隨點![]() 的移動而變化。
的移動而變化。
理由如下:如圖3,因為![]() ≌
≌ ![]() ,
,
所以![]() ,
,
因為![]() ,
,![]() ,
,
又因為![]() ,
,
所以![]() .
.
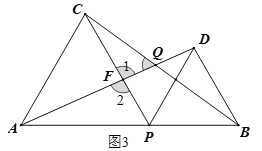
(3)因為旋轉的過程中,(2)中的兩個三角形的全等關系不變,所以角度不會變化.
所以![]() 的大小不會發生改變,始終等于
的大小不會發生改變,始終等于![]() .
.


 暑假作業海燕出版社系列答案
暑假作業海燕出版社系列答案 本土教輔贏在暑假高效假期總復習云南科技出版社系列答案
本土教輔贏在暑假高效假期總復習云南科技出版社系列答案 暑假作業北京藝術與科學電子出版社系列答案
暑假作業北京藝術與科學電子出版社系列答案科目:初中數學 來源: 題型:
【題目】如圖,平行四邊形ABCD中,AB=8cm,AD=12cm,點P在AD 邊上以每秒1cm的速度從點A向點D運動,點Q在BC邊上,以每秒4cm的速度從點C出發,在CB間往返運動,兩個點同時出發,當點P到達點D時停止(同時點Q也停止),在運動以后,以P、D、Q、B四點組成平行四邊形的次數有( )

A. 4次 B. 3次 C. 2次 D. 1次
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某汽車專賣店經銷某種型號的汽車.已知該型號汽車的進價為![]() 萬元/輛,經銷一段時間后發現:當該型號汽車售價定為
萬元/輛,經銷一段時間后發現:當該型號汽車售價定為![]() 萬元/輛時,平均每周售出
萬元/輛時,平均每周售出![]() 輛;售價每降低
輛;售價每降低![]() 萬元,平均每周多售出
萬元,平均每周多售出![]() 輛.
輛.
(1)當售價為![]() 萬元/輛時,平均每周的銷售利潤為___________萬元;
萬元/輛時,平均每周的銷售利潤為___________萬元;
(2)若該店計劃平均每周的銷售利潤是![]() 萬元,為了盡快減少庫存,求每輛汽車的售價.
萬元,為了盡快減少庫存,求每輛汽車的售價.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在等邊三角形ABC中,AB=12cm,動點P從點A出發以1cm/s的速度沿AC勻速運動,動點Q同時從點B出發以同樣的速度沿CB的延長線方向勻速運動,當點P到達點C時,點P,Q同時停止運動.設運動時間為ts,過點P作PE⊥AB于點E,連接PQ交AB于點D.
⑴當t為何值時,△CPQ為直角三角形?
⑵求DE的長.
⑶取線段BC的中點M,連接PM,將△CPM沿直線PM翻折,得到△C,PM,連接AC,,當t= 時,AC,的值最小,最小值為 .

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在ABCD中,過B點作BM⊥AC于點E,交CD于點M,過D點作DN⊥AC于點F,交AB于點N.
(1)求證:四邊形BMDN是平行四邊形;
(2)已知AF=12,EM=5,求AN的長.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知關于x的方程3x2-(a-3)x-a=0(a>0).
(1)求證:方程總有兩個不相等的實數根;
(2)若方程有一個根大于2,求a的取值范圍.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在我市“青山綠水”行動中,某社區計劃對面積為![]() 的區域進行綠化,經投標由甲、乙兩個工程隊來完成.已知甲隊每天能完成綠化的面積是乙隊每天能完成綠化面積的2倍,如果兩隊各自獨立完成面積為
的區域進行綠化,經投標由甲、乙兩個工程隊來完成.已知甲隊每天能完成綠化的面積是乙隊每天能完成綠化面積的2倍,如果兩隊各自獨立完成面積為![]() 區域的綠化時,甲隊比乙隊少用6天.
區域的綠化時,甲隊比乙隊少用6天.
(1)求甲、乙兩工程隊每天各能完成多少面積的綠化;
(2)若甲隊每天綠化費用是1.2萬元,乙隊每天綠化費用為0.5萬元,社區要使這次綠化的總費用不超過40萬元,則至少應安排乙工程隊綠化多少天?
查看答案和解析>>
科目:初中數學 來源: 題型:
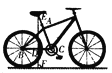
【題目】如圖所示的是一輛自行車的側面示意圖.已知車輪直徑為65 cm,車架中AC的長為42 cm,座桿AE的長為18 cm,點E,A,C在同一條直線上,后軸軸心B與中軸軸心C所在直線BC與地面平行,∠C=73°,求車座E到地面的距離EF.(結果精確到l cm,參考數據:sin 73°≈0.96,cos 73°≈0.29,tan 73°≈3.27)
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com