
【題目】小輝為了解市政府調整水價方案的社會反響,隨機訪問了自己居住在小區的部分居民,就“每月每戶的用水量”和“調價對用水行為改變”兩個問題進行調查,并把調查結果整理成下面的圖1,圖2.
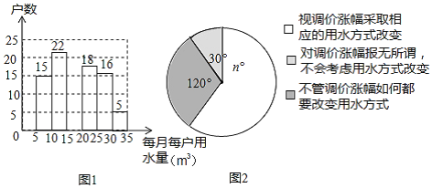
小輝發現每月每戶的用水量在![]() 之間,有7戶居民對用水價格調價漲幅抱無所謂,不用考慮用水方式的改變.根據小軍繪制的圖表和發現的信息,完成下列問題:
之間,有7戶居民對用水價格調價漲幅抱無所謂,不用考慮用水方式的改變.根據小軍繪制的圖表和發現的信息,完成下列問題:
(1)![]() ,小明調查了 戶居民,并補全圖1;
,小明調查了 戶居民,并補全圖1;
(2)每月每戶用水量的中位數落在 之間,眾數落在 之間;
(3)如果小明所在的小區有1200戶居民,請你估計“視調價漲幅采取相應的用水方式改變”的居民戶數多少?
【答案】(1)210,84,補圖見解析;(2)![]() ,
,![]() ;(3)700戶
;(3)700戶
【解析】
(1)利用![]() 即可求出n的值,利用“對用水價格調價漲幅抱無所謂,不用考慮用水方式的改變”的居民的數量除以相應的百分比即可求出調查的總數量,然后用總數量減去用水量在
即可求出n的值,利用“對用水價格調價漲幅抱無所謂,不用考慮用水方式的改變”的居民的數量除以相應的百分比即可求出調查的總數量,然后用總數量減去用水量在![]() ,
,![]() 的居民的數量,即可求出用水量在
的居民的數量,即可求出用水量在![]() 之間的居民的數量,即可補全圖1;
之間的居民的數量,即可補全圖1;
(2)根據中位數和眾數的概念即可得出答案;
(3)用總人數1200×樣本中“視調價漲幅采取相應的用水方式改變”的居民所占的百分比即可得出答案.
(1) ![]() ,
,
調查的居民的總數為![]() ,
,
用水量在![]() 之間的居民的數量為
之間的居民的數量為![]() ,
,
補全的圖1如圖:
(2)根據中位數的概念,因為共調查了84戶居民,每月每戶用水量的中位數為第41,42個數據的平均數,即中位數落在![]() 之間,由圖可知,用水量在
之間,由圖可知,用水量在![]() 的數據最多,所以眾數落在
的數據最多,所以眾數落在![]() 之間;
之間;
(3)∵![]() (戶),
(戶),
∴估計“視調價漲幅采取相應的用水方式改變”的居民戶數有700戶.


科目:初中數學 來源: 題型:
【題目】如圖,在Rt△ABC 中,∠C=90°,以BC為直徑的半圓交AB于點D,O是該半圓所在圓的圓心,E為線段AC上一點,且ED=EA.
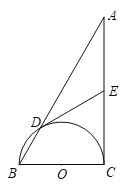
(1)求證:ED是⊙O的切線;
(2)若![]() ,∠A=30°,求⊙O的半徑.
,∠A=30°,求⊙O的半徑.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在以線段AB為直徑的⊙O上取一點,連接AC、BC.將△ABC沿AB翻折后得到△ABD.
(1)試說明點D在⊙O上;
(2)在線段AD的延長線上取一點E,使AB2=AC·AE.求證:BE為⊙O的切線;
(3)在(2)的條件下,分別延長線段AE、CB相交于點F,若BC=2,AC=4,求線段EF的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,![]() 中,
中,![]() .
.![]() . 將
. 將![]() 繞點
繞點![]() 順時針旋轉60°到點
順時針旋轉60°到點![]() ,點
,點![]() 與點
與點![]() 關于直線
關于直線![]() 對稱,連接
對稱,連接![]() ,
,![]() ,
,![]() .
.
(1)依題意補全圖形:
(2)判斷![]() 的形狀,并證明你的結論;
的形狀,并證明你的結論;
(3)請問在直線![]() 上是否存在點
上是否存在點![]() .使得
.使得![]() 恒成立若存在,請用文字描述出點
恒成立若存在,請用文字描述出點![]() 的準確位置,并畫圖證明;若不存在,請說明理由.
的準確位置,并畫圖證明;若不存在,請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
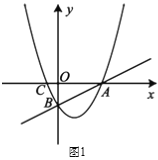
【題目】如圖![]() 所示,在平面直角坐標系
所示,在平面直角坐標系![]() 中,直線
中,直線![]() 與
與![]() 軸交于點
軸交于點![]() ,與
,與![]() 軸交于點
軸交于點![]() ,拋物線
,拋物線![]() 經過
經過![]() ,
,![]() 兩點,與
兩點,與![]() 軸的另一交點為點
軸的另一交點為點![]() .
.
(1)求拋物線的函數表達式;
(2)點![]() 為直線
為直線![]() 下方拋物線上一動點.
下方拋物線上一動點.
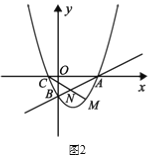
①如圖2所示,直線![]() 交線段
交線段![]() 于點
于點![]() ,求
,求![]() 的最小值;
的最小值;
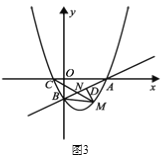
② 如圖3所示,連接![]() 過點
過點![]() 作
作![]() 于
于![]() ,是否存在點
,是否存在點![]() ,使得
,使得![]() 中的某個角恰好等于
中的某個角恰好等于![]() 的2倍?若存在,求點
的2倍?若存在,求點![]() 的坐標;若不存在,請說明理由.
的坐標;若不存在,請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】先閱讀,再填空解題:
(1)方程:![]() 的根是:
的根是:![]() ________,
________,![]() ________,則
________,則![]() ________,
________,![]() ________.
________.
(2)方程![]() 的根是:
的根是:![]() ________,
________,![]() ________,則
________,則![]() ________,
________,![]() ________.
________.
(3)方程![]() 的根是:
的根是:![]() ________,
________,![]() ________,則
________,則![]() ________,
________,![]() ________.
________.
(4)如果關于![]() 的一元二次方程
的一元二次方程![]() (
(![]() 且
且![]() 、
、![]() 、
、![]() 為常數)的兩根為
為常數)的兩根為![]() ,
,![]() ,
,
根據以上(1)(2)(3)你能否猜出:![]() ,
,![]() 與系數
與系數![]() 、
、![]() 、
、![]() 有什么關系?請寫出來你的猜想并說明理由.
有什么關系?請寫出來你的猜想并說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知點A(﹣3,y1),B(2,y2)均在拋物線y=ax2+bx+c上,點P(m,n)是該拋物線的頂點,若y1>y2≥n,則m的取值范圍是( )
A.﹣3<m<2B.﹣![]() <m<-
<m<-![]() C.m>﹣
C.m>﹣![]() D.m>2
D.m>2
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com