
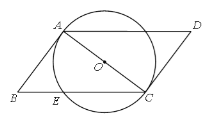
【題目】如圖,AC是⊙O的直徑,AB與⊙O相切于點A.四邊形ABCD是平行四邊形,BC交⊙O于點E.
(1)證明直線CD與⊙O相切;
(2)若⊙O的半徑為5 cm,弦CE的長為8 cm,求AB的長.
【答案】(1)見解析;(2) 7.5 cm.
【解析】
(1)根據題意,易得∠CAB=90°,又由四邊形ABCD是平行四邊形,結合平行四邊形的性質AB∥CD,可得∠CAB=∠ACD=90°,故直線CD與⊙O相切;
(2)連接AE,易得△CAE∽△CBA,進而可得![]() =
=![]() ,在Rt△CAE中,由勾股定理可得AE的值,代入關系式,可得答案.
,在Rt△CAE中,由勾股定理可得AE的值,代入關系式,可得答案.
解:(1)直線CD與⊙O相切.
理由如下:
∵AC是⊙O的直徑,AB與⊙O相切于點A,
∴AC⊥AB,∴∠CAB=90.
∵在□ABCD中,AB∥CD,∴∠ACD=90,
∴AC⊥CD.
∵點C在⊙O上,
∴直線CD與⊙O相切;
(2)如圖,連接AE,則AE⊥BC,
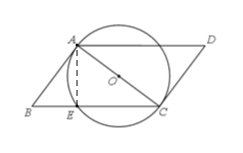
在Rt△CAE中,
AE=![]() =
=![]() =6 cm.
=6 cm.
由△CAE∽△CBA,得![]() =
=![]() ,
,
∴AB=7.5 cm.
故答案為:(1)證明過程見解析;(2)7.5 cm.


科目:初中數學 來源: 題型:
【題目】端午節期間,某食品店平均每天可賣出300只粽子,賣出1只粽子的利潤是1元.經調查發現,零售單價每降0.1元,每天可多賣出100只粽子.為了使每天獲取的利潤更多,該店決定把零售單價下降m(0<m<1)元.
(1)零售單價下降m元后,該店平均每天可賣出_____只粽子,利潤為_____元.
(2)在不考慮其他因素的條件下,當m定為多少時,才能使該店每天獲取的利潤是420元并且賣出的粽子更多?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在二次函數y=-x2+bx+c中,函數y與自變量x的部分對應值如下表:
x | …… | -2 | 0 | 3 | 4 | …… |
y | …… | -7 | m | n | -7 | …… |
則m、n的大小關系為( )
A. m>n B. m<n C. m=n D. 無法確定
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】對于函數![]() (k>0)有以下四個結論:
(k>0)有以下四個結論:
①這是y關于x的反比例函數;②當x>0時,y的值隨著x的增大而減小;③函數圖象與x軸有且只有一個交點;④函數圖象關于點(0,3)成中心對稱.
其中正確的是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在平面直角坐標系xOy中,對正方形ABCD及其內部的每個點進行如下操作:把每個點的橫、縱坐標都乘以同一個實數a,將得到的點先向右平移m個單位,再向上平移n個單位(m>0,n>0),得到正方形A'B'C'D'及其內部的點,其中點A、B的對應點分別為A',B'.已知正方形ABCD內部的一個點F經過上述操作后得到的對應點F'與點F重合,則點F的坐標是( )
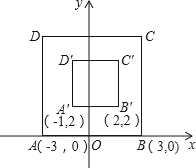
A. (1,4) B. (1,5) C. (﹣1,4) D. (4,1)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,四邊形ABCD中,∠A=∠B=90°,P是線段AB上的一個動點.
(1)若AD=2,BC=6,AB=8,且以A,D,P為頂點的三角形與以B,C,P為頂點的三角形相似,求AP的長;
(2)若AD=a,BC=b,AB=m,則當a,b,m滿足什么關系時,一定存在點P使△ADP∽△BPC?并說明理由.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在平面直角坐標系中,∠AOB=90°,∠OAB=30°,反比例函數y1=![]() 的圖象經過點A,反比例函數y2=
的圖象經過點A,反比例函數y2=![]() 的圖象經過點B,則下列關于m,n的關系正確的是( )
的圖象經過點B,則下列關于m,n的關系正確的是( )

A. m=-3n B. m=-![]() n C. m=-
n C. m=-![]() n D. m=
n D. m=![]() n
n
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com