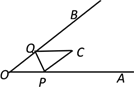
【題目】如圖，已知∠AOB＝45°，點P、Q分別是邊OA，OB上的兩點，將∠O沿PQ折疊，點O落在平面內點C處.若折疊后PC⊥QB，則∠OPQ的度數是____________.
【答案】22.5°或112.5°
【解析】分析：根據題意畫出符合要求的圖形，如下圖1和圖2，分點C在OA下方和OB上方兩種情況結合折疊的性質及已知條件解答即可.
詳解：
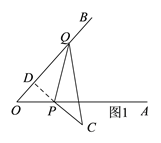
（1）如圖1，當點C在OA的下方時，延長CP交OB于點D，
∵CP⊥OB，
∴∠ODC=90°，
∵∠AOB=45°，
∴∠DPC=45°，
∴∠OPQ+∠CPQ=45°+180°=225°，
∵由折疊的性質可知∠OPQ=∠CPQ，
∴∠OPQ=112.5°；
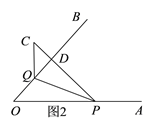
（2）如圖2，當點C在OB的上方時，
∵PC⊥OB，
∴∠ODP=90°，
又∵∠AOB=45°，
∴∠OPQ+∠CPQ=∠OPC=45°，
∵由折疊的性質可知∠OPQ=∠CPQ，
∴∠OPQ=22.5°.
綜上所述，當PC⊥OB時，∠OPQ的度數為112.5°或22.5°.
故答案為：112.5°或22.5°.
科目：初中數學 來源： 題型：
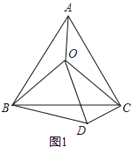
【題目】（1）如圖1，O是等邊△ABC內一點，連接OA、OB、OC，且OA=3，OB=4，OC=5，將△BAO繞點B順時針旋轉后得到△BCD，連接OD．求：
①旋轉角是____度；
②線段OD的長為_____；
③求∠BDC的度數．
（2）如圖2所示，O是等腰直角△ABC（∠ABC=90°）內一點，連接OA、OB、OC，∠A0B=135，OA=1，0B=2，求0C的長.
小明同學借用了圖1的方法，將△BAO繞點B順時針旋轉后得到△BCD，請你繼續用小明的思路解答，或是選擇自己的方法求解.
查看答案和解析>>
科目：初中數學 來源： 題型：
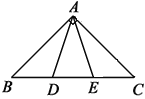
【題目】如圖，在△ABC中， ∠BAC=90°， AB=AC=2
，點D，E均在邊BC上，且∠DAE=45°，若BD=1，則DE=__________．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，在四邊形ABCD中，∠A=110°，∠B=85°將△BMN沿著MN翻折，得到△FMN，若MF∥AD，FN∥DC，則∠C的度數為（ ）
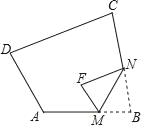
A. 70° B. 80° C. 90° D. 100°
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】定義一種對正整數n的“F”運算：①當n為奇數時，F（n）=3n+1；②當n為偶數時，F（n）=
（其中k是使F（n）為奇數的正整數）……，兩種運算交替重復進行，例如，取n=24，則：
若n=13，則第2018次“F”運算的結果是（ ）
A. 1 B. 4 C. 2018 D. 42018
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，將△ABC放在每個小正方形的邊長為1的網格中，點A，點B，點C均落在格點上．
（1）計算AC2+BC2的值等于 ；
（2）請在如圖所示的網格中，用無刻度的直尺，畫出一個平行四邊形ABEF，使得該平行四邊形的面積等于16；
（3）請在如圖所示的網格中，用無刻度的直尺，畫出一個矩形ABMN，使得該矩形的面積等于AC2+BC2．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，已知A（n，﹣2），B（1，4）是一次函數y=kx+b的圖象和反比例函數y=
的圖象的兩個交點，直線AB與y軸交于點C．
（1）求反比例函數和一次函數的關系式；
（2）求△AOC的面積；
（3）求不等式kx+b﹣＜0的解集．（直接寫出答案）
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】為了加強學生的安全意識，某校組織了學生參加安全知識競賽．從中抽取了部分學生成績（得分數取正整數，滿分為100分）進行統計，已知A組的頻數a比B組的頻數b小24，繪制統計頻數分布直方圖（未完成）和扇形圖如下，請解答下列問題：
（1）樣本容量為：______，a為______；
（2）n為________，E組所占比例為________；
（3）補全頻數分布直方圖；
（4）若成績在80分以上記作優秀，全校共有2000名學生，估計成績優秀學生有_________名．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
