
【題目】寧波某公司經銷一種綠茶,每千克成本為![]() 元.市場調查發現,在一段時間內,銷售量
元.市場調查發現,在一段時間內,銷售量![]() (千克)隨銷售單價
(千克)隨銷售單價![]() (元/千克)的變化而變化,具體關系式為:
(元/千克)的變化而變化,具體關系式為:![]() .設這種綠茶在這段時間內的銷售利潤為
.設這種綠茶在這段時間內的銷售利潤為![]() (元),解答下列問題:
(元),解答下列問題:
(1)求![]() 與
與![]() 的關系式;
的關系式;
(2)當銷售單價![]() 取何值時,銷售利潤
取何值時,銷售利潤![]() 的值最大,最大值為多少?
的值最大,最大值為多少?
(3)如果物價部門規定這種綠茶的銷售單價不得高于![]() 元/千克,公司想要在這段時間內獲得
元/千克,公司想要在這段時間內獲得![]() 元的銷售利潤,銷售單價應定為多少元?
元的銷售利潤,銷售單價應定為多少元?
【答案】(1)y=-2![]() +340x-12000 ;(2)當x=85時,y的值最大,且最大值為2450;(3)當銷售單價為75元時,可獲得銷售利潤2250元.
+340x-12000 ;(2)當x=85時,y的值最大,且最大值為2450;(3)當銷售單價為75元時,可獲得銷售利潤2250元.
【解析】
(1)因為y=(x-50)w,w=-2x+240
故y與x的關系式為y=-2x2+340x-12000.
(2)用配方法化簡函數式求出y的最大值即可.
(3)令y=2250時,求出x的解即可.
(1)解:由題意可知:y=(x-50)×w=(x-50)×(-2x+240)=-2![]() +340x-12000
+340x-12000
∴y 與 x 的關系式為:y=(x-50)×w=(x-50)×(-2x+240)=-2![]() +340x-12000
+340x-12000
(2)解:由(1)得:y=-2![]() +340x-12000 ,
+340x-12000 ,
配方得:y=-2![]() +2450 ;
+2450 ;
∵函數開口向下,且對稱軸為x=85,
∴當x=85時,y的值最大,且最大值為2450.
(3)解:當y=2250時,可得方程 -2![]() +2450=2250;
+2450=2250;
解得:![]() =75,
=75,![]() =95 ;
=95 ;
由題意可知:x≤90,
∴![]() =95 不合題意,應該舍去。
=95 不合題意,應該舍去。
∴當銷售單價為75元時,可獲得銷售利潤2250元。


 華東師大版一課一練系列答案
華東師大版一課一練系列答案科目:初中數學 來源: 題型:
【題目】如圖,有一張矩形紙片,長10cm,寬6cm,在它的四角各減去一個同樣的小正方形,然后折疊成一個無蓋的長方體紙盒.若紙盒的底面(圖中陰影部分)面積是32cm2,求剪去的小正方形的邊長.設剪去的小正方形邊長是xcm,根據題意可列方程為( )

A. 10×6﹣4×6x=32 B. (10﹣2x)(6﹣2x)=32
C. (10﹣x)(6﹣x)=32 D. 10×6﹣4x2=32
查看答案和解析>>
科目:初中數學 來源: 題型:
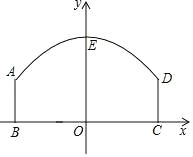
【題目】如圖,一隧道的橫截面是由一段拋物線及矩形的三邊圍成的,隧道寬BC=10米,矩形部分高AB=3米,拋物線型的最高點E離地面OE=6米,按如圖建立一個以BC為x軸,OE為y軸的直角坐標系.
(1)求拋物線的解析式;
(2)如果該隧道內設有雙車道,現有一輛貨運卡車高4.5米,寬3米,這輛貨運卡車能順利通過隧道嗎?
查看答案和解析>>
科目:初中數學 來源: 題型:
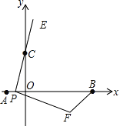
【題目】如圖,在平面直角坐標系中,已知點A、B、C的坐標分別為(﹣1,0),(5,0),(0,2).若點P從A點出發,沿x軸正方向以每秒1個單位長度的速度向B點移動,連接PC并延長到點E,使CE=PC,將線段PE繞點P順時針旋轉90°得到線段PF,連接FB.若點P在移動的過程中,使△PBF成為直角三角形,則點F的坐標是________.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】拋物線![]() 的頂點為
的頂點為![]() ,與
,與![]() 軸的一個交點
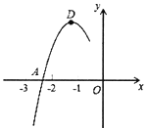
軸的一個交點![]() 在點(-3, 0)和(-2 ,0)之間,其部分圖象如圖,則以下結論:①
在點(-3, 0)和(-2 ,0)之間,其部分圖象如圖,則以下結論:①![]() <0;②
<0;②![]() <0;③
<0;③![]() =2;④方程
=2;④方程![]() 有兩個相等的實數根,其中正確結論的個數為________個.
有兩個相等的實數根,其中正確結論的個數為________個.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在平面直角坐標系xOy中,對于點P(a,b)和點Q(a,b′),給出如下定義:
若b′=![]() ,則稱點Q為點P的理想點.例如:點(1,2)的理想點的坐標是(1,﹣2),點(﹣2,3)的理想點的坐標是(﹣2,3).
,則稱點Q為點P的理想點.例如:點(1,2)的理想點的坐標是(1,﹣2),點(﹣2,3)的理想點的坐標是(﹣2,3).
(1)點(![]() ,﹣1)理想點的坐標是_____;若點C在函數y=2x2的圖象上,則它的理想點是A(1,﹣2),B(﹣1,2)中的哪一個?_____;
,﹣1)理想點的坐標是_____;若點C在函數y=2x2的圖象上,則它的理想點是A(1,﹣2),B(﹣1,2)中的哪一個?_____;
(2)若點P在函數y=﹣2x+4(﹣2≤x≤k,k>﹣2)的圖象上,其理想點為Q:
①若其理想點Q的縱坐標b′的取值范圍是﹣6≤b′≤10,求k的值;
②在①的條件下,若點P的理想點Q都不在反比例函數y=![]() (m<0,x>0)上,求m的取值范圍.
(m<0,x>0)上,求m的取值范圍.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在矩形ABCD中,E是AD邊的中點,BE⊥AC于點F,連接DF,分析下列五個結論:①△AEF∽△CAB;②CF=2AF;③DF=DC;④S四邊形CDEF=![]() S△ABF,其中正確的結論有________個。
S△ABF,其中正確的結論有________個。

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com