
【題目】天水市某企業接到一批粽子生產任務,按要求在19天內完成,約定這批粽子的出廠價為每只4元,為按時完成任務,該企業招收了新工人,設新工人李紅第x天生產的粽子數量為y只,y與x滿足如下關系:![]() .
.
(1)李紅第幾天生產的粽子數量為260只?
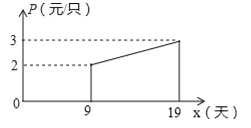
(2)如圖,設第x天生產的每只粽子的成本是p元,p與x之間的關系可用圖中的函數圖象來刻畫,若李紅第x天創造的利潤為w元,求w與x之間的函數表達式,并求出第幾天的利潤最大?最大利潤是多少元?(利潤=出廠價﹣成本)
【答案】(1)第10天;(2)第13天的利潤最大,最大利潤是786元.
【解析】
試題分析:(1)令函數y=20x+60的函數值為260,然后求對應的自變量的值即可;
(2)先利用函數圖象得到P與x的關系:0≤x≤9時,p=2;當9<x≤19時,解析式為y=![]() x+
x+![]() ,然后分類討論:當0≤x≤5時,w=(4﹣2)32x;當5<x≤9時,w=(4﹣2)(20x+60);當9<x≤19時,w=[4﹣(
,然后分類討論:當0≤x≤5時,w=(4﹣2)32x;當5<x≤9時,w=(4﹣2)(20x+60);當9<x≤19時,w=[4﹣(![]() x+
x+![]() )](20x+60),再利用一次函數和二次函數的性質求出三種情況下的w的最大值,于是比較大小即可得到利潤的最大值.
)](20x+60),再利用一次函數和二次函數的性質求出三種情況下的w的最大值,于是比較大小即可得到利潤的最大值.
試題解析:(1)設李紅第x天生產的粽子數量為260只,根據題意得20x+60=260,解得x=10.
答:李紅第10天生產的粽子數量為260只;
(2)根據圖象得當0≤x≤9時,p=2;
當9<x≤19時,設解析式為y=kx+b,把(9,2),(19,3)代入得:![]() ,解得:
,解得: ,所以p=
,所以p=![]() ,①當0≤x≤5時,w=(4﹣2)32x=64x,x=5時,此時w的最大值為320(元);
,①當0≤x≤5時,w=(4﹣2)32x=64x,x=5時,此時w的最大值為320(元);
②當5<x≤9時,w=(4﹣2)(20x+60)=40x+120,x=9時,此時w的最大值為480(元);
③當9<x≤19時,w=[4﹣(![]() )](20x+60)=
)](20x+60)=![]() =
=![]() ,x=13時,此時w的最大值為786(元);
,x=13時,此時w的最大值為786(元);
綜上所述,第13天的利潤最大,最大利潤是786元.


 閱讀快車系列答案
閱讀快車系列答案科目:初中數學 來源: 題型:
【題目】如圖,已知數軸上的點A表示的數為6,點B表示的數為﹣4,點C到點A、點B的距離相等,動點P從點B出發,以每秒2個單位長度的速度沿數軸向右勻速運動,設運動時間為 x ( x 大于0)秒.![]()
(1)點C表示的數是;
(2)當 ![]() 秒時,點P到達點A處?
秒時,點P到達點A處?
(3)運動過程中點P表示的數是(用含字母 ![]() 的式子表示);
的式子表示);
(4)當P,C之間的距離為2個單位長度時,求 x 的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】把下列各數填在相應的表示集合的大括號里.
4,0.5,﹣1 ![]() ,10%,﹣5,﹣3.14,0,
,10%,﹣5,﹣3.14,0, ![]() ,+2018
,+2018
(1)正整數集合{…}
(2)分數集合{…}
(3)負有理數集合{…}
(4)整數集合{…}.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】襄陽市某企業積極響應政府“創新發展”的號召,研發了一種新產品.已知研發、生產這種產品的成本為30元/件,且年銷售量y(萬件)關于售價x(元/件)的函數解析式為:![]() .
.
(1)若企業銷售該產品獲得的年利潤為W(萬元),請直接寫出年利潤W(萬元)關于售價x(元/件)的函數解析式;
(2)當該產品的售價x(元/件)為多少時,企業銷售該產品獲得的年利潤最大?最大年利潤是多少?
(3)若企業銷售該產品的年利潤不少于750萬元,試確定該產品的售價x(元/件)的取值范圍.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,△ABC三個頂點的坐標分別為A(1,1),B(4,2),C(3,4).
(1)請畫出將△ABC向左平移4個單位長度后得到的圖形△A1B1C1;
(2)請畫出△ABC關于原點O成中心對稱的圖形△A2B2C2;
(3)在x軸上找一點P,使PA+PB的值最小,請直接寫出點P的坐標.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知拋物線C:y=(x+2)[t(x+1)-(x+3)],其中-7≤t≤-2,且無論t 取任何符合條件的實數,點A,P 都在拋物線C 上.
(1)當t=-5時,求拋物線C 的對稱軸;
(2)當-60≤n≤-30 時,判斷點(1,n)是否在拋物線C上, 并說明理由;
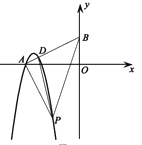
(3)如圖,若點A在x軸上,過點A作線段AP的垂線交y軸于點B,交拋物線C于點D,當點D的縱坐標為m+![]() 時,求S△PAD的最小值.
時,求S△PAD的最小值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com