
【題目】如圖,二次函數y=![]() x2+bx﹣
x2+bx﹣![]() 的圖象與x軸交于點A(﹣3,0)和點B,以AB為邊在x軸上方作正方形ABCD,點P是x軸上一動點,連接DP,過點P作DP的垂線與y軸交于點E.
的圖象與x軸交于點A(﹣3,0)和點B,以AB為邊在x軸上方作正方形ABCD,點P是x軸上一動點,連接DP,過點P作DP的垂線與y軸交于點E.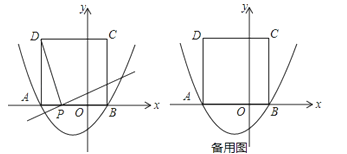
(1)b的值及點D的坐標。
(2)線段AO上是否存在點P(點P不與A、O重合),使得OE的長為1;
(3)在x軸負半軸上是否存在這樣的點P,使△PED是等腰三角形?若存在,請求出點P的坐標及此時△PED與正方形ABCD重疊部分的面積;若不存在,請說明理由.
【答案】解:(1)∵點A(﹣3,0)在二次函數y=![]() x2+bx﹣
x2+bx﹣![]() 的圖象上,
的圖象上,
∴0=![]() ﹣3b﹣
﹣3b﹣![]() ,解得b=1,
,解得b=1,
∴二次函數解析式為y=![]() x2+x﹣
x2+x﹣![]() =
=![]() (x+3)(x﹣1),
(x+3)(x﹣1),
∴點B(1,0),AB=1﹣(﹣3)=4,
∵四邊形ABCD為正方形,
∴AD=AB=4,
∴點D(﹣3,4),
故答案為:1;(﹣3,4).
(2)直線PE交y軸于點E,如圖1,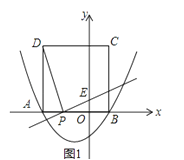
假設存在點P,使得OE的長為1,設OP=a,則AP=3﹣a,
∵DP⊥AE,∠APD+∠DPE+∠EPO=180°,
∴∠EPO=90°﹣∠APD=∠ADP,
tan∠ADP=![]() =
=![]() ,tan∠EPO=
,tan∠EPO=![]() =
=![]() ,
,
∴![]() =
=![]() ,即a2﹣3a+4=0,
,即a2﹣3a+4=0,
△=(﹣3)2﹣4×4=﹣7,無解
故線段AO上不存在點P(點P不與A、O重合),使得OE的長為1.
(3)假設存在這樣的點P,DE交x軸于點M,如圖2,
∵△PED是等腰三角形,
∴DP=PE,
∵DP⊥PE,四邊形ABCD為正方形
∴∠EPO+∠APD=90°,∠DAP=90°,∠PAD+∠APD=90°,
∴∠EPO=∠PDA,∠PEO=∠DPA,
在△PEO和△DAP中,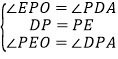 ,
,
∴△PEO≌△DAP,
∴PO=DA=4,OE=AP=PO﹣AO=4﹣3=1,
∴點P坐標為(﹣4,0).
∵DA⊥x軸,
∴DA∥EO,
∴∠ADM=∠OEM(兩直線平行,內錯角相等),
又∵∠AMD=∠OME(對頂角),
∴△DAM∽EOM,
∴![]() =
=![]() =
=![]() ,
,
∵OM+MA=OA=3,
∴MA=![]() ×3=
×3=![]() ,
,
△PED與正方形ABCD重疊部分△ADM面積為![]() ×AD×AM=
×AD×AM=![]() ×4×
×4×![]() =
=![]() .
.
答:存在這樣的點P,點P的坐標為(﹣4,1),此時△PED與正方形ABCD重疊部分的面積為![]() .
.
【解析】(1)利用點在二次函數圖象上,代入即可求得b,將二次函數換成交點式,即能得出B點的坐標,由AD=AB可算出D點坐標;
(2)假設存在,由DP⊥AE,找出∠EPO=∠PDA,利用等角的正切相等,可得出一個關于OP長度的一元二次方程,由方程無解可得知不存在這樣的點;
(3)利用角和邊的關系,找到全等,再利用三角形相似,借助相似比即可求得AM,求出△ADM的面積即是所求.


 七彩題卡口算應用一點通系列答案
七彩題卡口算應用一點通系列答案科目:初中數學 來源: 題型:
【題目】如圖是二次函數y=ax2+bx+c圖象的一部分,其對稱軸為x=﹣1,且過點(﹣3,0)下列說法:
①abc<0;②2a﹣b=0;③4a+2b+c<0;④若(﹣5,y1),(2,y2)是拋物線上的兩點,則y1>y2 .
其中說法正確的是( )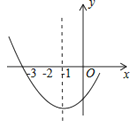
A.①②
B.②③
C.②③④
D.①②④
查看答案和解析>>
科目:初中數學 來源: 題型:
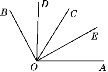
【題目】如圖,OD平分∠BOC,OE平分∠AOC,∠BOC=60°,∠AOC=58°.
(1)求出∠AOB及其補角的度數;
(2)①請求出∠DOC和∠AOE的度數;
②判斷∠DOE與∠AOB是否互補,并說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
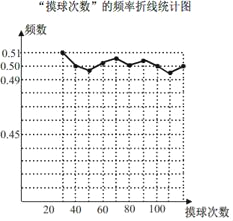
【題目】在一個不透明袋子中裝有顏色不同的黑、白兩種球共40個球,小穎做摸球實驗,她將盒子里面的球攪勻后從中隨機摸出一個球記下顏色,再把它放回盒子中,不斷重復上述過程.如圖是“摸到白球”的頻率折線統計圖:
(1)根據統計圖,估算盒子里黑、白兩種顏色的球各多少個?
(2)如果要使摸到白球的概率為![]() ,需要往盒子里再放入多少個白球?
,需要往盒子里再放入多少個白球?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,四邊形ABCD中,AD=CD,∠DAB=∠ACB=90°,過點D作DE⊥AC,垂足為F,DE與AB相交于點E.
(1)求證:ABAF=CBCD;
(2)已知AB=15cm,BC=9cm,P是線段DE上的動點.設DP=x cm,梯形BCDP的面積為ycm2 .
①求y關于x的函數關系式.
②y是否存在最大值?若有求出這個最大值,若不存在請說明理由.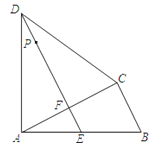
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,正方形ABCD的邊長為1,AC,BD是對角線,將△DCB繞著點D順時針旋轉45°得到△DGH,HG交AB于點E,連接DE交AC于點F,連接FG.則下列結論:
①四邊形AEGF是菱形;②△HED的面積是1﹣![]() ;③∠AFG=112.5°;④BC+FG=
;③∠AFG=112.5°;④BC+FG=![]() .其中正確的結論是( )
.其中正確的結論是( )

A. ①②③ B. ①②④ C. ①③④ D. ②③④
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在平面直角坐標系中,點A,B分別在y軸和x軸上,∠ABO=60°,在坐標軸上找一點P,使得△PAB是等腰三角形,則符合條件的點P共有( )
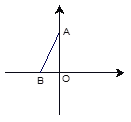
A. 3個 B. 4個 C. 5個 D. 6個
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在![]() 中,∠ACB=90°,AC=BC=4,D為BC的中點,
中,∠ACB=90°,AC=BC=4,D為BC的中點, ![]() ,垂足為E.過點B作BF//AC交DE的延長線于點F,連接CF,AF.現有如下結論:
,垂足為E.過點B作BF//AC交DE的延長線于點F,連接CF,AF.現有如下結論:
①BF=2;②![]() ;③AD平分∠CAB;④AF=
;③AD平分∠CAB;④AF=![]() ;⑤∠CAF=∠CFB.其中正確的結論是( )
;⑤∠CAF=∠CFB.其中正確的結論是( )
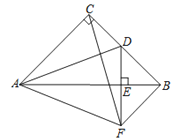
A. ①②③ B. ①②④ C. ②③④⑤ D. ①②④⑤
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com