【題目】如圖所示，已知拋物線y＝ax＋bx＋c與x軸負半軸交于A、B兩點，與y軸交于點C，且OB＝
，CB＝2，∠CAO＝30°，求拋物線的解析式和它的頂點坐標。
【答案】拋物線解析式為:
,頂點坐標是(
).
【解析】
在Rt△BOC中,根據OB＝
,CB＝2,由勾股定理可得:OC=3, 在Rt△AOC中,根據∠CAO＝30°,OC=3,根據30°角所對直角邊等于斜邊的一半, 可得AC=6,再根據勾股定理可得:OA=
,所以點A(
),B(
),C(0,3),根據拋物線與x軸負半軸交于A、B兩點,與y軸交于點C,可設拋物線解析式為:
,把點C坐標代入可得:
,解得:
,所以拋物線解析式為:,所以頂點坐標是()
在Rt△BOC中,因為OB＝,CB＝2,
由勾股定理可得:OC=3,
在Rt△AOC中,因為∠CAO＝30°,OC=3,
所以 AC=6,
根據勾股定理可得:OA=,
所以點A(),B(),C(0,3),
因為拋物線與x軸負半軸交于A、B兩點,與y軸交于點C,
可設拋物線解析式為:,
把點C坐標代入可得:
,
解得:,
所以拋物線解析式為:,
所以頂點坐標是()
科目：初中數學 來源： 題型：
【題目】在平面直角坐標系中，A點坐標為（3，4），將線段OA繞原點O逆時針旋轉90°得到線段OA′，則點A′的坐標是（ ）
A. （﹣4，3） B. （﹣3，4）
C. （3，﹣4） D. （4，﹣3）
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】有兩個可以自由轉動的均勻轉盤
，都被分成了3等份，并在每份內均標有數字，如圖所示．規則如下：
①分別轉動轉盤；
②兩個轉盤停止后，將兩個指針所指份內的數字相乘（若指針停止在等份線上，那么重轉一次，直到指針指向某一份為止）．
【1】用列表法或樹狀圖分別求出數字之積為3的倍數和數字之積為5的倍數的概率；
【2】小明和小亮想用這兩個轉盤做游戲，他們規定：數字之積為3的倍數時，小明得2分；數字之積為5的倍數時，小亮得3分．這個游戲對雙方公平嗎？請說明理由；認為不公平的，試修改得分規定，使游戲對雙方公平．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】一項工程，甲，乙兩公司合做，12天可以完成，共需付施工費102000元；如果甲，乙兩公司單獨完成此項工程，乙公司所用時間是甲公司的1.5倍，乙公司每天的施工費比甲公司每天的施工費少1500元．
（1）甲，乙兩公司單獨完成此項工程，各需多少天？
（2）若讓一個公司單獨完成這項工程，哪個公司的施工費較少？
查看答案和解析>>
科目：初中數學 來源： 題型：
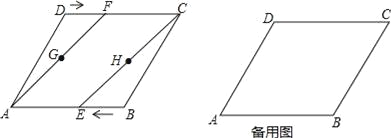
【題目】如圖，在菱形ABCD中，AB=4cm，∠BAD=60°．動點E、F分別從點B、D同時出發，以1cm/s的速度向點A、C運動，連接AF、CE，取AF、CE的中點G、H，連接GE、FH．設運動的時間為ts（0＜t＜4）．
（1）求證：AF∥CE；
（2）當t為何值時，四邊形EHFG為菱形；
（3）試探究：是否存在某個時刻t，使四邊形EHFG為矩形，若存在，求出t的值，若不存在，請說明理由．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，△ABC 是等邊三角形，BD 是 AC 邊上的高，延長 BC 到 E使 CE＝CD，則圖中等腰三角形的個數是（）
A.1 個B.2 個C.3 個D.4 個
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，△ABE，△BCD均為等邊三角形，點A，B，C在同一條直線上，連接AD，EC，AD與EB相交于點M，BD與EC相交于點N，下列說法正確的有：___________
①AD=EC；②BM=BN；③MN∥AC；④EM=MB．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，直角坐標系內的梯形
（
為原點）中
，
，
，
，
．
求經過，
，
三點的拋物線的解析式；
延長
交拋物線于點
，求線段
的長；
在的條件下，動點
、
分別從、同時出發，都以每秒
個單位的速度運動，其中點沿
由向運動，點沿
由由運動（其中一個點運動到終點后，另一個點運動也隨之停止），過點作
交
于點
，連接
．設動點運動的時間為
秒，請你探索：當時間為何值時，
中有一個角是直角．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
