
【題目】如圖,AOB是一條直線,∠AOC=60°,OD,OE分別是∠AOC和∠BOC的平分線,則圖中互補的角有( ) 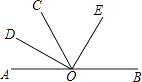
A.5對
B.6對
C.7對
D.8對
【答案】D
【解析】解:∠BOC=180°﹣∠AOC=180°﹣60°=120°,
∵OD,OE分別是∠AOC和∠BOC的平分線,
∴∠AOD=∠COD=30°,∠COE=∠BOE=60°,
∴∠AOE=∠BOC=120°,∠DOE=90°,∠DOB=150°,
則∠AOD+∠DOB=180°,∠COD+∠DOB=180°,∠AOC+∠BOC=180°,∠COE+∠BOC=180°,∠BOE+∠BOC=180°,∠AOE+∠BOE=180°,∠AOE+∠AOC=180°,∠AOE+∠COE=180°.
總之有8對互補的角.
故選D.
【考點精析】認真審題,首先需要了解余角和補角的特征(互余、互補是指兩個角的數量關系,與兩個角的位置無關).


 閱讀快車系列答案
閱讀快車系列答案科目:初中數學 來源: 題型:
【題目】問題提出;怎樣計算1×2+2×3+3×4+…+(n﹣1)×n呢?
材料學習
計算1+2+3…+n
因為1= ![]() (1×2﹣0×1);2=
(1×2﹣0×1);2= ![]() (2×3﹣1×2);3=
(2×3﹣1×2);3= ![]() (3×4﹣2×3)
(3×4﹣2×3)
…,n= ![]() [n(n+1)﹣(n﹣1)n]
[n(n+1)﹣(n﹣1)n]
所以1+2+3+…+n
= ![]() (1×2﹣0×1)+
(1×2﹣0×1)+ ![]() (2×3﹣1×2)+
(2×3﹣1×2)+ ![]() (3×4﹣2×3)+…+
(3×4﹣2×3)+…+ ![]() [n(n+1)﹣(n﹣1)n]
[n(n+1)﹣(n﹣1)n]
= ![]() [1×2﹣0×1+2×3﹣1×2+3×4﹣2×3+…+n(n+1)﹣(n﹣1)n]=
[1×2﹣0×1+2×3﹣1×2+3×4﹣2×3+…+n(n+1)﹣(n﹣1)n]= ![]() n(n+1)
n(n+1)
(1)探究應用
觀察規律:①1×2= ![]() (1×2×3﹣0×12);②2×3=
(1×2×3﹣0×12);②2×3= ![]() (2×3×4﹣1×2×3);
(2×3×4﹣1×2×3);
③3×4= ![]() (3×4×5﹣2×3×4);…
(3×4×5﹣2×3×4);…
猜想歸納:
根據(1)中觀察的規律直接寫出:4×5= ![]() ()
()
(n﹣1)×n= ![]() []
[]
問題解決:
1×2+2×3+3×4+4×5…+(n﹣1)×n
= ![]() (1×2×3﹣0×1×2)+
(1×2×3﹣0×1×2)+ ![]() (2×3×4﹣1×2×3)+
(2×3×4﹣1×2×3)+ ![]() (3×4×5﹣2×3×4)+…+
(3×4×5﹣2×3×4)+…+ ![]() []
[]
=
(2)拓展延伸
根據上面的規律,請直接寫出1×2×3+2×3×4+3×4×5+…+(n﹣2)(n﹣1)n= .
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某大橋采用低塔斜拉橋橋型(如甲圖),圖乙是從圖甲引申出的平面圖,假設你站在橋上測得拉索AB與水平橋面的夾角是30°,拉索CD與水平橋面的夾角是60°,兩拉索頂端的距離BC為2米,兩拉索底端距離AD為20米,請求出立柱BH的長.(結果精確到0.1米, ![]() ≈1.73)
≈1.73)

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某校為進行危房改造,政府最近將在某校搭建板房,從某廠調拔了用于搭建板房的板材5600m3和鋁材2210m3 , 計劃用這些材料在某校搭建甲、乙兩種規格的板房共100間.若搭建一間甲型 板房或一間乙型板房所需板材和鋁材的數量如表所示:
板房規格 | 板材數量(m3) | 鋁材數量(m3) |
甲型 | 40 | 30 |
乙型 | 60 | 20 |
請你根據以上信息,設計出甲、乙兩種板房的搭建方案.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com