
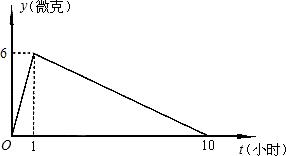
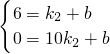
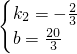 ,y=-
,y=- t+
t+
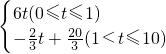

 )
) t+
t+ =4,∴t=4.
=4,∴t=4. 小時后開始有效,有效時間長為:4-
小時后開始有效,有效時間長為:4- =
= (小時).
(小時). t1+
t1+ =4,t1=4(小時).
=4,t1=4(小時). t2+
t2+ -
- (t2-4)+
(t2-4)+ =4,解得t2=9(小時).
=4,解得t2=9(小時). (t3-4)+
(t3-4)+ -
- (t3-9)+
(t3-9)+ =4,
=4, (小時).
(小時).

科目:初中數學 來源: 題型:
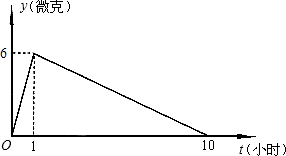
查看答案和解析>>
科目:初中數學 來源:2012年北師大版初中數學八年級下5.2數據的收集練習卷(解析版) 題型:解答題
2003年5月,一場抗擊非典肺炎的 “戰爭”在全國各地進行著,為了獲得每天感染非典患者,疑似病例患者的數據,需要對十二億多人進行普查嗎?你認為采取什么調查方式更適合?請結合實際情況談談你的想法。
查看答案和解析>>
科目:初中數學 來源:遼寧省期末題 題型:解答題
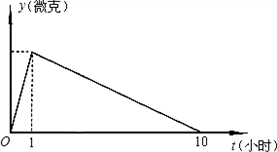
查看答案和解析>>
科目:初中數學 來源:2003年全國中考數學試題匯編《一次函數》(03)(解析版) 題型:解答題
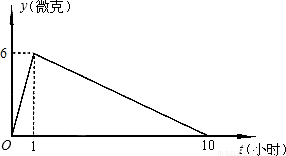
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com