
 分別為AB、OB邊上的動點它們同時分別從點A、O向B點勻速運動,速度均為1cm/秒,設P、Q移動時間為t(0≤t≤4)
分別為AB、OB邊上的動點它們同時分別從點A、O向B點勻速運動,速度均為1cm/秒,設P、Q移動時間為t(0≤t≤4) =
= =5cm,
=5cm,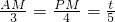 ,
, t,OM=OA-AM=3-
t,OM=OA-AM=3- t,
t, t,3-
t,3- t);
t); ×t×(3-
×t×(3- t)=-
t)=- t2+
t2+ t
t (t-
(t- )2+
)2+ ,
, 時,S有最大值,最大值為
時,S有最大值,最大值為 ;
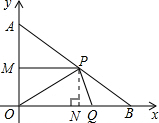
;
 ,
, t)2=
t)2= t(t-
t(t- t),
t), t,OQ=t,
t,OQ=t, t,
t, cm/s,
cm/s, t=
t= t•
t• ,
,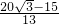 .
. OQ分別列式求解即可得到Q點運動速度和時間t.
OQ分別列式求解即可得到Q點運動速度和時間t.

 名師指導期末沖刺卷系列答案
名師指導期末沖刺卷系列答案科目:初中數學 來源: 題型:
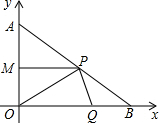 分別為AB、OB邊上的動點它們同時分別從點A、O向B點勻速運動,速度均為1cm/秒,設P、Q移動時間為t(0≤t≤4)
分別為AB、OB邊上的動點它們同時分別從點A、O向B點勻速運動,速度均為1cm/秒,設P、Q移動時間為t(0≤t≤4)查看答案和解析>>
科目:初中數學 來源: 題型:
 如圖,在Rt△AOB中,∠ABO=90°,OB=4,AB=8,且反比例函數y=
如圖,在Rt△AOB中,∠ABO=90°,OB=4,AB=8,且反比例函數y=| k | x |
查看答案和解析>>
科目:初中數學 來源: 題型:
 (2013•咸寧)如圖,在Rt△AOB中,OA=OB=3
(2013•咸寧)如圖,在Rt△AOB中,OA=OB=3| 2 |
| 2 |
| 2 |
查看答案和解析>>
科目:初中數學 來源: 題型:

查看答案和解析>>
科目:初中數學 來源: 題型:
 (2013•南崗區一模)如圖,在Rt△AOB中,∠AOB=90°,且AO=8,BO=6,P是線段AB上一個動點,PE⊥A0于E,PF⊥B0于F.設
(2013•南崗區一模)如圖,在Rt△AOB中,∠AOB=90°,且AO=8,BO=6,P是線段AB上一個動點,PE⊥A0于E,PF⊥B0于F.設查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com