
【題目】已知拋物線y=x2﹣2x+a(a<0)與y軸相交于點A,頂點為M.直線y=![]() x﹣a分別與x軸,y軸相交于B,C兩點,并且與直線AM相交于點N.
x﹣a分別與x軸,y軸相交于B,C兩點,并且與直線AM相交于點N.
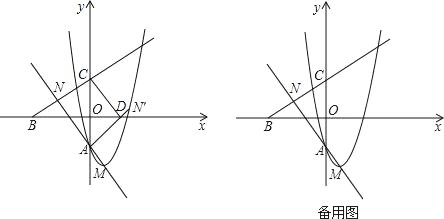
(1)試用含a的代數式分別表示點M與N的坐標;
(2)如圖,將△NAC沿y軸翻折,若點N的對應點N′恰好落在拋物線上,AN′與x軸交于點D,連接CD,求a的值和四邊形ADCN的面積;
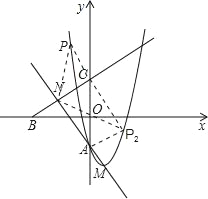
(3)在拋物線y=x2﹣2x+a(a<0)上是否存在一點P,使得以P,A,C,N為頂點的四邊形是平行四邊形?若存在,求出P點的坐標;若不存在,試說明理由.
【答案】(1)M(1,a﹣1),N(![]() a,﹣
a,﹣![]() a);(2)a=
a);(2)a=![]() , S四邊形ADCN
, S四邊形ADCN![]() ;(3)詳見解析.
;(3)詳見解析.
【解析】分析:(1)、已知了拋物線的解析式,不難用公式法求出M的坐標為(1,a-1).由于拋物線過A點,因此A的坐標是(0,a).根據A,M的坐標,用待定系數法可得出直線AM的解析式.聯(lián)立方程組即可求出N的坐標為;(2)、根據折疊的性質不難得出N與N′正好關于y軸對稱,得出N′的坐標.由于N′在拋物線上,因此將N′的坐標代入拋物線的解析式中即可得出a的值.也就能確定N,C的坐標.求四邊形ADCN的面積,可分成△ANC和△ADC兩部分來求.已經求得了A,C,N的坐標,可求出AC的長以及N,D到y軸的距離.也就能求出△ANC和△ADC的面積,進而可求出四邊形ADCN的面積;(3)、本題可分兩種情況進行討論:①當P在y軸左側時,如果使以P,N,A,C為頂點的四邊形為平行四邊形,那么P需要滿足的條件是PN平行且相等于AC,也就是說,如果N點向上平移AC個單位即-2a后得到的點就是P點.然后將此時P的坐標代入拋物線中,如果沒有解說明不存在這樣的點P,如果能求出a的值,那么即可求出此時P的坐標.②當P在y軸右側時,P需要滿足的條件是PN與AC應互相平分(平行四邊形的對角線互相平分),那么NP必過原點,且關于原點對稱.那么可得出此時P的坐標,然后代入拋物線的解析式中按①的方法求解即可.
詳解:解:(1)M(1,a﹣1),N(![]() a,﹣
a,﹣![]() a);
a);
(2)∵由題意得點N與點N′關于y軸對稱,∴N′(﹣![]() a,﹣
a,﹣![]() a).
a).
將N′的坐標代入y=x2﹣2x+a得:﹣![]() a=
a=![]() a2+
a2+![]() a+a,
a+a,
∴a1=0(不合題意,舍去),![]() .∴N(﹣3,
.∴N(﹣3, ![]() ),
),
∴點N到y(tǒng)軸的距離為3. ∵A(0,﹣![]() ),N′(3,
),N′(3, ![]() ),
),
∴直線AN′的解析式為![]() ,它與x軸的交點為D(
,它與x軸的交點為D(![]() ) ∴點D到y(tǒng)軸的距離為
) ∴點D到y(tǒng)軸的距離為![]() .
.
∴S四邊形ADCN=S△ACN+S△ACD=![]() ;
;
(3)存在,理由如下:
①當點P在y軸的左側時,若ACPN是平行四邊形,則PN![]() AC,
AC,
則把N向上平移﹣2a個單位得到P,坐標為(![]() a,﹣
a,﹣![]() a),代入拋物線的解析式,
a),代入拋物線的解析式,
得:﹣![]() a=
a=![]() a2﹣
a2﹣![]() a+a, 解得a1=0(不舍題意,舍去),a2=﹣
a+a, 解得a1=0(不舍題意,舍去),a2=﹣![]() ,
,
則P(﹣![]() ,
, ![]() );
);
②當點P在y軸的右側時,若APCN是平行四邊形,則AC與PN互相平分,
則OA=OC,OP=ON. 則P與N關于原點對稱, 則P(﹣![]() a,
a, ![]() a);
a);
將P點坐標代入拋物線解析式得: ![]() a=
a=![]() a2+
a2+![]() a+a, 解得a1=0(不合題意,舍去),a2=﹣
a+a, 解得a1=0(不合題意,舍去),a2=﹣![]() ,
,
則P(![]() ,﹣
,﹣![]() ).
).
故存在這樣的點P(﹣![]() ,
, ![]() )或P(
)或P(![]() ,﹣
,﹣![]() ),能使得以P,A,C,N為頂點的四邊形是平行四邊形.
),能使得以P,A,C,N為頂點的四邊形是平行四邊形.


 導學與測試系列答案
導學與測試系列答案 新非凡教輔沖刺100分系列答案
新非凡教輔沖刺100分系列答案科目:初中數學 來源: 題型:
【題目】某校為了解學生的安全意識情況,在全校范圍內隨機抽取部分學生進行問卷調查,根據調查結果,把學生的安全意識分成“淡薄”、“一般”、“較強”、“很強”四個層次,并繪制成如下兩幅尚不完整的統(tǒng)計圖.

根據以上信息,解答下列問題:
(1)這次調查一共抽取了 名學生,其中安全意識為“很強”的學生占被調查學生總數的百分比是 ;
(2)請將條形統(tǒng)計圖補充完整;
(3)該校有1800名學生,現要對安全意識為“淡薄”、“一般”的學生強化安全教育,根據調查結果,估計全校需要強化安全教育的學生約有 名.
查看答案和解析>>
科目:初中數學 來源: 題型:
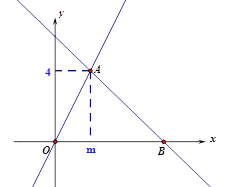
【題目】如圖,在平面直角坐標系xOy中,一次函數![]() 的圖象與正比例函數
的圖象與正比例函數![]() 的圖象交于點A(m,4).
的圖象交于點A(m,4).
(1)求m、n的值;
(2)設一次函數![]() 的圖象與x軸交于點B,求△AOB的面積;
的圖象與x軸交于點B,求△AOB的面積;
(3)直接寫出使函數![]() 的值小于函數
的值小于函數![]() 的值的自變量x的取值范圍.
的值的自變量x的取值范圍.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】直線AB,CD交于點O,將一個三角板的直角頂點放置于點O處,使其兩條直角邊OE,OF,分別位于OC的兩側.若OC平分∠BOF,OE平分∠COB.
(1)求∠BOE的度數;
(2)寫出圖中∠BOE的補角,并說明理由.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某檢修小組從A地出發(fā),在東西方向的馬路上檢修線路,如果規(guī)定向東行駛為正,向西行駛為負,一天中七次行駛紀錄如下.(單位:km)
第一次 | 第二次 | 第三次 | 第四次 | 第五次 | 第六次 | 第七次 |
-4 | +8 | -9 | +8 | +6 | -5 | -2 |
(1)求收工時距A地多遠?
(2)若每km耗油0.4升,問一天共耗油多少升?
查看答案和解析>>
科目:初中數學 來源: 題型:
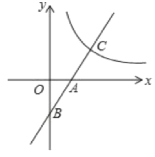
【題目】如圖,已知一次函數y=2x2的圖象與x,y軸分別交于點A,B,與反比例函數y=![]() (x>0)的圖象交于點C,且AB=AC,則k的值為()
(x>0)的圖象交于點C,且AB=AC,則k的值為()
A.5B.4C.3D.2
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在平面直角坐標系中,一次函數![]() 的圖像與反比例函數
的圖像與反比例函數![]() 的圖像交于第一、三象限內的
的圖像交于第一、三象限內的![]() 、
、![]() 兩點,與
兩點,與![]() 軸交于點
軸交于點![]() ,點
,點![]() 在
在![]() 軸負半軸上,
軸負半軸上,![]() ,且四邊形
,且四邊形![]() 是平行四邊形,點
是平行四邊形,點![]() 的縱坐標為
的縱坐標為![]() .
.
(1)求該反比例函數和一次函數的表達式;
(2)連接![]() ,求
,求![]() 的面積;
的面積;
(3)直接寫出關于![]() 的不等式
的不等式![]() 的解集.
的解集.

查看答案和解析>>
科目:初中數學 來源: 題型:
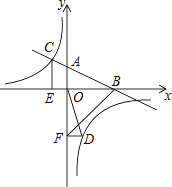
【題目】如圖,在平面直角坐標系中,直線AB與x軸交于點B,與y軸交于點A,與反比例函數![]() 的圖象在第二象限交于點C,CE⊥x軸,垂足為點E,
的圖象在第二象限交于點C,CE⊥x軸,垂足為點E,![]() ,OB=4,OE=2.
,OB=4,OE=2.
(1)求反比例函數的解析式;
(2)若點D是反比例函數圖象在第四象限上的點,過點D作DF⊥y軸,垂足為點F連接OD、BF,如果![]() ,求點D的坐標.
,求點D的坐標.
查看答案和解析>>
湖北省互聯(lián)網違法和不良信息舉報平臺 | 網上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com