
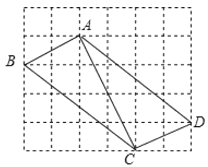
【題目】如圖,在邊長為1的小正方形組成的網格中,![]() 的三個頂點均在格點上,請按要求完成下列各題:
的三個頂點均在格點上,請按要求完成下列各題:

(1)畫線段![]() ,且使
,且使![]() ,連接
,連接![]() ;
;
(2)線段![]() 的長為________,
的長為________,![]() 的長為________,
的長為________,![]() 的長為________;
的長為________;
(3)![]() 是________三角形,四邊形
是________三角形,四邊形![]() 的面積是________;
的面積是________;
(4)若點![]() 為
為![]() 的中點,
的中點,![]() 為
為![]() ,則
,則![]() 的度數為________.
的度數為________.
【答案】(1)見解析;(2)![]() ,
,![]() ,5;(3)直角,10;(4)
,5;(3)直角,10;(4)![]()
【解析】
(1)根據題意,畫出AD∥BC且使AD=BC,連接CD;
(2)在網格中利用直角三角形,先求AC ![]() 的值,再求出AC的長,CD的長,AD的長;
的值,再求出AC的長,CD的長,AD的長;
(3)利用勾股定理的逆定理判斷直角三角形,再求出四邊形ABCD的面積;
(4)把問題轉化到Rt△ACB中,利用直角三角形斜邊上的中線可知BE=AE=EC,根據等腰三角形性質即可解題.
(1)如圖所示:AD、CD為所求作
(2)根據勾股定理得:![]()
故答案為:![]() ;
;![]() ;5
;5
(3)∵![]() ,
,![]()
∴![]()
∴![]() 是直角三角形,∠ACD=90°
是直角三角形,∠ACD=90°
∴四邊形![]() 的面積是:
的面積是:![]()
故答案為:直角;10
(4)∵![]() ,
,![]()
∴四邊形ABCD是平行四邊形
∴AB//CD
∴∠BAC=∠ACD=90°
在Rt△ACD中,![]() 為
為![]() 的中點
的中點
∴AE=BE=CE, ∠ABC+∠ACB=90°
∴∠ACB=∠EAC=27°
∴∠ABC =63°
故答案為:![]()


 第1卷單元月考期中期末系列答案
第1卷單元月考期中期末系列答案科目:初中數學 來源: 題型:
【題目】已知關于![]() 的一元二次方程
的一元二次方程![]() .
.
(1)![]() 為何值時,方程有一根為零?
為何值時,方程有一根為零?
(2)![]() 為何值時,方程的兩個根互為相反數?
為何值時,方程的兩個根互為相反數?
(3)是否存在![]() ,使方程的兩個根互為倒數?若存在,請求出
,使方程的兩個根互為倒數?若存在,請求出![]() 的值;不存在,請說明理由.
的值;不存在,請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】為解決中小學大班額問題,東營市各縣區今年將改擴建部分中小學,某縣計劃對A、B兩類學校進行改擴建,根據預算,改擴建2所A類學校和3所B類學校共需資金7800萬元,改擴建3所A類學校和1所B類學校共需資金5400萬元.
(1)改擴建1所A類學校和1所B類學校所需資金分別是多少萬元?
(2)該縣計劃改擴建A、B兩類學校共10所,改擴建資金由國家財政和地方財政共同承擔.若國家財政撥付資金不超過11800萬元;地方財政投入資金不少于4000萬元,其中地方財政投入到A、B兩類學校的改擴建資金分別為每所300萬元和500萬元.請問共有哪幾種改擴建方案?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,拋物線![]() (a≠0)的圖象與x軸交于A、B兩點,與y軸交于C點,已知B點坐標為(4,0).
(a≠0)的圖象與x軸交于A、B兩點,與y軸交于C點,已知B點坐標為(4,0).
(1)求拋物線的解析式;
(2)試探究△ABC的外接圓的圓心位置,并求出圓心坐標;
(3)若點M是線段BC下方的拋物線上一點,求△MBC的面積的最大值,并求出此時M點的坐標.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在△ABC中,∠BAC=90°,∠ABC=∠ACB,點D在直線BC上運動(不與點B、C重合),點E在射線AC上運動,且∠ADE=∠AED,設∠DAC=n.
(1)如圖①,當點D在邊BC上時,且n等于30°,則∠BAD= ,∠CDE= ;
(2)如圖②,當點D運動到點B左側時,其他條件不變,請猜想∠BAD和∠CDE的數量關系,并說明理由;
(3)當點D運動到點C的右側時,其他條件不變,∠BAD和∠CDE還滿足(2)中的數量關系嗎?請在圖③中畫出圖形,并說明理由.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】兩個反比例函數y=![]() (k>1)和y=
(k>1)和y=![]() 在第一象限內的圖象如圖所示,點P在y=
在第一象限內的圖象如圖所示,點P在y=![]() 的圖象上,PC⊥x軸于點C,交y=
的圖象上,PC⊥x軸于點C,交y=![]() 的圖象于點A,PD⊥y軸于點D,交y=
的圖象于點A,PD⊥y軸于點D,交y=![]() 的圖象于點B,BE⊥x軸于點E,當點P在y=
的圖象于點B,BE⊥x軸于點E,當點P在y=![]() 圖象上運動時,以下結論:①BA與DC始終平行;②PA與PB始終相等;③四邊形PAOB的面積不會發生變化;④△OBA的面積等于四邊形ACEB的面積.其中一定正確的是_____(填序號)
圖象上運動時,以下結論:①BA與DC始終平行;②PA與PB始終相等;③四邊形PAOB的面積不會發生變化;④△OBA的面積等于四邊形ACEB的面積.其中一定正確的是_____(填序號)

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com