
【題目】如圖,已知![]() 是
是![]() 的切線,
的切線,![]() 是
是![]() 的直徑,連接
的直徑,連接![]() 交
交![]() 于點
于點![]() ,在
,在![]() 上截取
上截取![]() ,在
,在![]() 中,連接
中,連接![]() ,交
,交![]() 于點
于點![]() .
.
(1)求證:![]() ;
;
(2)連接![]() ,
,![]() ,當
,當![]() 時,四邊形
時,四邊形![]() 是菱形.
是菱形.
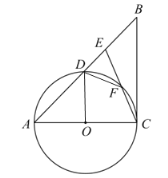
【答案】(1)見解析;(2)30°
【解析】
(1)連接AF,根據直徑所對的圓周角是直角可得∠AFC=90°,從而得出∠FAC+∠ACF=90°,然后根據三線合一可得∠BAC=2∠FAC,然后根據切線的性質可知∠BCE+∠ACF=90°,從而證出結論;
(2)連接OF,根據題意,易證當△OCF為等邊三角形時,此時OC= FC=FD= OD,即四邊形![]() 是菱形,從而求出∠OCF=60°,然后根據直角三角形的性質即可求出結論.
是菱形,從而求出∠OCF=60°,然后根據直角三角形的性質即可求出結論.
解:(1)連接AF
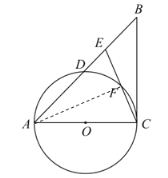
∵AC為直徑
∴∠AFC=90°
∴∠FAC+∠ACF=90°
∵![]()
∴∠BAC=2∠FAC
∵![]() 是
是![]() 的切線,
的切線,
∴∠ACB=90°
∴∠BCE+∠ACF=90°
∴∠FAC=∠BCE
∴∠BAC=2∠BCE
(2)連接OF
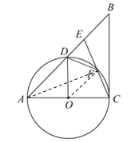
∵∠CAF=∠EAF
∴FC=FD
∵OC=OD=OF,
∴當△OCF為等邊三角形時,此時OC= FC=FD= OD,即四邊形![]() 是菱形
是菱形
∴∠OCF=60°
∴∠CAF=90°-∠OCF=30°
∴∠CAE=2∠CAF=60°
∴∠B=90°-∠CAE=30°
即當![]() 30°時,四邊形
30°時,四邊形![]() 是菱形
是菱形
故答案為:30°.


 53隨堂測系列答案
53隨堂測系列答案科目:初中數學 來源: 題型:
【題目】由于2020年新型冠狀病毒的襲擊,不得不推遲開學,但停課不停學,各地都開展了網課.某中學為了解學生上網課情況,開學后從全校七年級學生中隨機抽取部分學生進行了數學科目的測試(把測試結果分為四個等級:A級:優秀;B級:良好;C級:合格;D級:不合格),并將測試記錄繪成如下兩幅完全不同的統計圖,請根據統計圖中的信息解答下列問題:
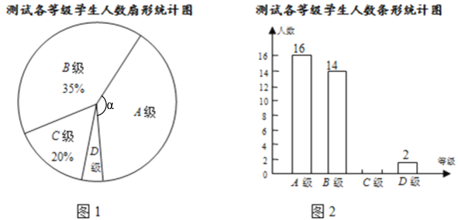
(1)本次抽樣測試的學生數是多少?
(2)求圖1中A級扇形的圓心角∠α的度數,并把圖2中的條形統計圖補充完成;
(3)該中學七年級共有1200名學生,如果全部參加這次數學科目測試,請估計不合格的人數.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某公司經過市場調查,發現某種運動服的銷量與售價是一次函數關系,具體信息如下表:
售價(元/件) | 200 | 210 | 220 | 230 | … |
月銷量(件) | 200 | 180 | 160 | 140 | … |
已知該運動服的進價為每件150元.
(1)售價為![]() 元,月銷量為
元,月銷量為![]() 件;
件;
①求![]() 關于
關于![]() 的函數關系式;
的函數關系式;
②若銷售該運動服的月利潤為![]() 元,求
元,求![]() 關于
關于![]() 的函數關系式,并求月利潤最大時的售價;
的函數關系式,并求月利潤最大時的售價;
(2)由于運動服進價降低了![]() 元,商家決定回饋顧客,打折銷售,這時月銷量與調整后的售價仍滿足(1)中函數關系式.結果發現,此時月利潤最大時的售價比調整前月利潤最大時的售價低15元,則
元,商家決定回饋顧客,打折銷售,這時月銷量與調整后的售價仍滿足(1)中函數關系式.結果發現,此時月利潤最大時的售價比調整前月利潤最大時的售價低15元,則![]() 的值是多少?
的值是多少?
查看答案和解析>>
科目:初中數學 來源: 題型:
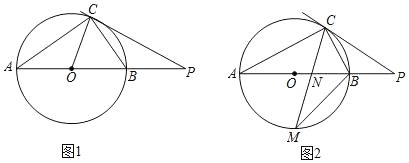
【題目】已知,AB是⊙O的直徑,點C在⊙O上,點P是AB延長線上一點,連接CP.
(1)如圖1,若∠PCB=∠A.
①求證:直線PC是⊙O的切線;
②若CP=CA,OA=2,求CP的長;
(2)如圖2,若點M是弧AB的中點,CM交AB于點N,MNMC=9,求BM的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某文具店準備購進A、B兩種品牌的文具袋進行銷售,若購進A品牌文具袋和B品牌文具袋各5個共花費120元,購進A品牌文具袋3個和B品牌文具袋4個共花費88元.
(1)求購進A品牌文具袋和B品牌文具袋的單價;
(2)若該文具店購進了A,B兩種品牌的文具袋共100個,其中A品牌文具袋售價為12元,B品牌文具袋售價為23元,設購進A品牌文具袋x個,獲得總利潤為w元.
①求w關于x的函數關系式;
②要使銷售文具袋的利潤最大,且所獲利潤不低于進貨價格的45%,請你幫該文具店設計一個進貨方案,并求出其所獲利潤的最大值.
查看答案和解析>>
科目:初中數學 來源: 題型:
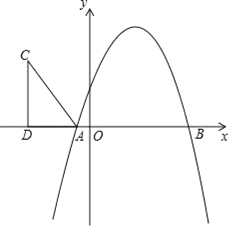
【題目】如圖,拋物線y=-x2+bx+c與x軸相交于A(-1,0),B(5,0)兩點.
(1)求拋物線的解析式;
(2)在第二象限內取一點C,作CD垂直x軸于點D,鏈接AC,且AD=5,CD=8,將Rt△ACD沿x軸向右平移m個單位,當點C落在拋物線上時,求m的值;
(3)在(2)的條件下,當點C第一次落在拋物線上記為點E,點P是拋物線對稱軸上一點.試探究:在拋物線上是否存在點Q,使以點B、E、P、Q為頂點的四邊形是平行四邊形?若存在,請出點Q的坐標;若不存在,請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
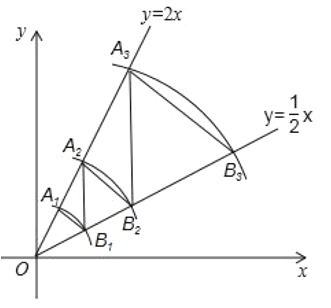
【題目】如圖,在平面直角坐標系中,點A1的坐標為(1,2),以點O為圓心,以OA1長為半徑畫弧,交直線![]() 于點B1.過B1點作B1A2∥y軸,交直線y=2x于點A2,以O為圓心,以OA2長為半徑畫弧,交直線
于點B1.過B1點作B1A2∥y軸,交直線y=2x于點A2,以O為圓心,以OA2長為半徑畫弧,交直線![]() 于點B2;過點B2作B2A3∥y軸,交直線y=2x于點A3,以點O為圓心,以OA3長為半徑畫弧,交直線
于點B2;過點B2作B2A3∥y軸,交直線y=2x于點A3,以點O為圓心,以OA3長為半徑畫弧,交直線![]() 于點B3;過B3點作B3A4∥y軸,交直線y=2x于點A4,以點O為圓心,以OA4長為半徑畫弧,交直線
于點B3;過B3點作B3A4∥y軸,交直線y=2x于點A4,以點O為圓心,以OA4長為半徑畫弧,交直線![]() 于點B4,…按照如此規律進行下去,點B2020的坐標為__________.
于點B4,…按照如此規律進行下去,點B2020的坐標為__________.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖1,已知拋物線y=﹣x2+2x+3與x軸交于A、B兩點,與y軸交于點C,頂點為D,連接BC
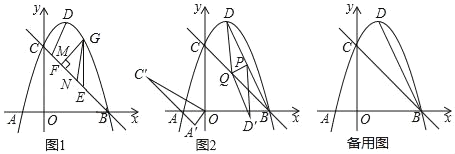
(1)點G是直線BC上方拋物線上一動點(不與B、C重合),過點G作y軸的平行線交直線BC于點E,作GF⊥BC于點F,點M、N是線段BC上兩個動點,且MN=EF,連接DM、GN.當△GEF的周長最大時,求DM+MN+NG的最小值;
(2)如圖2,連接BD,點P是線段BD的中點,點Q是線段BC上一動點,連接DQ,將△DPQ沿PQ翻折,且線段D′P的中點恰好落在線段BQ上,將△AOC繞點O逆時針旋轉60°得到△A′OC′,點T為坐標平面內一點,當以點Q、A′、C′、T為頂點的四邊形是平行四邊形時,求點T的坐標.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,Rt△ABE中,∠B=90°,AB=BE,將△ABE繞點A逆時針旋轉45°,得到△AHD,過D作DC⊥BE交BE的延長線于點C,連接BH并延長交DC于點F,連接DE交BF于點O.下列結論:①DE平分∠HDC;②DO=OE;③H是BF的中點;④BC-CF=2CE;⑤CD=HF,其中正確的有( )
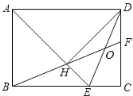
A.5個B.4個C.3個D.2個
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com