
【題目】在一條不完整的數軸上從左到右有點A,B,C,其中AB=2,BC=1,如圖所示,設點A,B,C所對應數的和是p.
(1)若以B為原點,則點A,C所對應的數分別為_____和_____,p的值為_____.若以C為原點,p的值為_____;
(2)若原點O在圖中數軸上點C的右邊,且CO=28,求p;
(3)若原點O在圖中數軸上點C的右邊,且CO=a,求p(用含a的代數式表示).
(4)若原點O在圖中數軸上線段BC上,且CO=a,求p(用含a的代數式表示).利用此結果計算當a=0.5時,p的值.
![]()
【答案】(1)﹣2、1、﹣1、﹣4;(2)-88;(3)p=﹣3a﹣4;(4)p= 3a﹣4,當a=0.5時,p=﹣2.5.
【解析】
(1)根據以B為原點,則C表示1,A表示﹣2,進而得到p的值;根據以C為原點,則A表示﹣3,B表示﹣1,進而得到p的值;
(2)根據原點O在圖中數軸上點C的右邊,且CO=28,可得C表示﹣28,B表示﹣29,A表示﹣31,據此可得p的值.
(3)若原點O在圖中數軸上點C的右邊,且CO=a,可得C的值為﹣a,B的值為﹣a﹣1,A的值為﹣a﹣3,據此可得p的值;
(4)若原點O在圖中數軸上線段BC上,且CO=a,可得C的值為a,B的值為﹣(1﹣a)=a﹣1,A的值為a﹣3,據此得出p的值,代入計算可得答案.
(1)若以B為原點,則點A所對應的數為﹣2、點C對應的數為1,此時p=﹣2+0+1=﹣1;
若以C為原點,則點A所對應的數為﹣3、點B對應的數為﹣1,此時p=﹣3﹣1+0=﹣4.
故答案為:﹣2、1、﹣1、﹣4;
(2)根據題意知,C的值為﹣28,B的值為﹣29,A的值為﹣31,則p=﹣28﹣29﹣31=﹣88;
(3)根據題意知,C的值為﹣a,B的值為﹣a﹣1,A的值為﹣a﹣3,則p=﹣a﹣a﹣1﹣a﹣3=﹣3a﹣4;
(4)根據題意知,C的值為a,B的值為﹣(1﹣a)=a﹣1,A的值為a﹣3,p=a+a﹣1+a﹣3=3a﹣4,當a=0.5時,p=3×0.5﹣4=﹣2.5.


科目:初中數學 來源: 題型:
【題目】每逢金秋送爽之時,正是大閘蟹上市的旺季,也是吃蟹的最好時機,可謂膏肥黃美.九月份,某經銷商購進一批雌蟹、雄蟹共1000只,進價均為每只40元,然后以雌蟹每只75元、雄蟹每只60元的價格售完,共獲利29000元.
(1)求該經銷商分別購進雌蟹、雄蟹各多少只?
(2)民間有“九雌十雄”的說法,即九月吃雌蟹,十月吃雄蟹.十月份,在進價不變的情況下該經銷商決定調整價格,將雌蟹的價格在九月份的基礎上下調a%(降價后售價不低于進價),雄蟹的價格上漲 ![]() a%,同時雌蟹的銷量較九月下降了
a%,同時雌蟹的銷量較九月下降了 ![]() a%,雄蟹的銷量上升了25%,結果十月份的銷售額比九月份增加了1000元,求a的值.
a%,雄蟹的銷量上升了25%,結果十月份的銷售額比九月份增加了1000元,求a的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
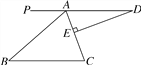
【題目】如圖,AD∥BC,∠BAC=70°,DE⊥AC于點E,∠D=20°.
(1)求∠B的度數,并判斷△ABC的形狀;
(2)若延長線段DE恰好過點B,試說明DB是∠ABC的平分線.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,點A、B、C是圓O上的三點,且四邊形ABCO是平行四邊形,OF⊥OA交圓O于點F,則∠CBF等于( ) 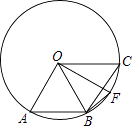
A.12.5°
B.15°
C.20°
D.22.5°
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】下列變形中:
①由方程![]() =2去分母,得x﹣12=10;
=2去分母,得x﹣12=10;
②由方程![]() x=
x=![]() 兩邊同除以
兩邊同除以![]() ,得x=1;
,得x=1;
③由方程6x﹣4=x+4移項,得7x=0;
④由方程2﹣![]() 兩邊同乘以6,得12﹣x﹣5=3(x+3).
兩邊同乘以6,得12﹣x﹣5=3(x+3).
錯誤變形的個數是( )個.
A. 4 B. 3 C. 2 D. 1
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】設三角形三個內角的度數分別為x,y,z,如果其中一個角的度數是另一個角的度數的2倍,那么我們稱數對(y,z)(y≤z)是x的和諧數對.例:當x=150°時,對應的和諧數對有一個,它為(10,20);當x=66時,對應的和諧數對有二個,它們為(33,81),(38,76).當對應的和諧數對(y,z)有三個時,此時x的取值范圍是____________.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某地區的電力資源豐富,并且得到了較好的開發.該地區一家供電公司為了鼓勵居民用電,采用分段計費的方法來計算電費.月用電量x(度)與相應電費y(元)之間的函數圖像如圖所示.
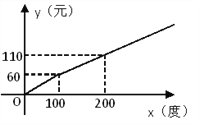
(1)月用電量為100度時,應交電費 元;
(2)當x≥100時,求y與x之間的函數關系式;
(3)月用電量為260度時,應交電費多少元?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】一個自然數的立方,可以分裂成若干個連續奇數的和。例如:![]() 和
和![]() 分別可以按如圖所示的方式“分裂”成2個、3個和4個連續奇數的和,即
分別可以按如圖所示的方式“分裂”成2個、3個和4個連續奇數的和,即![]() =3+5;
=3+5;![]() =7+9+11;
=7+9+11;![]() =13+15+17+19;…;若
=13+15+17+19;…;若![]() 也按照此規律來進行“分裂”,則
也按照此規律來進行“分裂”,則![]() “分裂”出的奇數中,最大的奇數是______.
“分裂”出的奇數中,最大的奇數是______.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】定義[p,q]為一次函數y=px+q的特征數.
(1)若特征數是[k-1,k2-1]的一次函數為正比例函數,求k的值;
(2)在平面直角坐標系中,有兩點A(-m,0),B(0,-2m),且△OAB的面積為4(O為原點),若一次函數的圖象過A,B兩點,求該一次函數的特征數.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com