
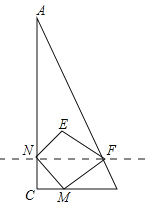
【題目】如圖,已知△ABC中,∠C=90°,點M從點C出發沿CB方向以1cm/s的速度勻速運動,到達點B停止運動,在點M的運動過程中,過點M作直線MN交AC于點N,且保持∠NMC=45°,再過點N作AC的垂線交AB于點F,連接MF,將△MNF關于直線NF對稱后得到△ENF,已知AC=8cm,BC=4cm,設點M運動時間為t(s),△ENF與△ANF重疊部分的面積為y(cm2).
(1)在點M的運動過程中,能否使得四邊形MNEF為正方形?如果能,求出相應的t值;如果不能,說明理由;
(2)求y關于t的函數解析式及相應t的取值范圍;
(3)當y取最大值時,求sin∠NEF的值.
【答案】(1)![]() ;(2)
;(2) ;(3)
;(3)![]() .
.
【解析】
試題分析:(1)由已知得出CN=CM=t,FN∥BC,得出AN=8﹣t,由平行線證出△ANF∽△ACB,得出對應邊成比例求出NF=![]() AN=
AN=![]() (8﹣t),由對稱的性質得出∠ENF=∠MNF=∠NMC=45°,MN=NE,OE=OM=CN=t,由正方形的性質得出OE=ON=FN,得出方程,解方程即可;
(8﹣t),由對稱的性質得出∠ENF=∠MNF=∠NMC=45°,MN=NE,OE=OM=CN=t,由正方形的性質得出OE=ON=FN,得出方程,解方程即可;
(2)分兩種情況:①當0<t≤2時,由三角形面積得出![]() ;
;
②當2<t≤4時,作GH⊥NF于H,由(1)得:NF=![]() (8﹣t),GH=NH,GH=2FH,得出GH=
(8﹣t),GH=NH,GH=2FH,得出GH=![]() NF=
NF=![]() (8﹣t),由三角形面積得出
(8﹣t),由三角形面積得出![]() (2<t≤4);
(2<t≤4);
(3)當點E在AB邊上時,y取最大值,連接EM,則EF=BF,EM=2CN=2CM=2t,EM=2BM,得出方程,解方程求出CN=CM=2,AN=6,得出BM=2,NF=![]() AN=3,因此EM=2BM=4,作FD⊥NE于D,由勾股定理求出EB=
AN=3,因此EM=2BM=4,作FD⊥NE于D,由勾股定理求出EB=![]() =
=![]() ,求出EF=
,求出EF=![]() EB=
EB=![]() ,由等腰直角三角形的性質和勾股定理得出DF=
,由等腰直角三角形的性質和勾股定理得出DF=![]() HF=
HF=![]() ,在Rt△DEF中,由三角函數定義即可求出sin∠NEF的值.
,在Rt△DEF中,由三角函數定義即可求出sin∠NEF的值.
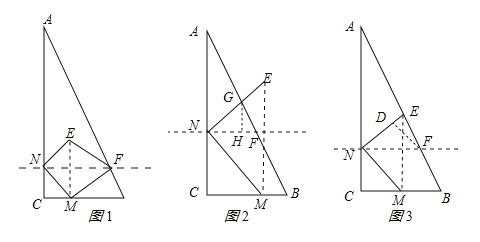
試題解析:(1)能使得四邊形MNEF為正方形;理由如下:
連接ME交NF于O,如圖1所示:
∵∠C=90°,∠NMC=45°,NF⊥AC,∴CN=CM=t,FN∥BC,∴AN=8﹣t,△ANF∽△ACB,∴![]() =2,∴NF=
=2,∴NF=![]() AN=
AN=![]() (8﹣t),由對稱的性質得:∠ENF=∠MNF=∠NMC=45°,MN=NE,OE=OM=CN=t,∵四邊形MNEF是正方形,∴OE=ON=FN,∴t=
(8﹣t),由對稱的性質得:∠ENF=∠MNF=∠NMC=45°,MN=NE,OE=OM=CN=t,∵四邊形MNEF是正方形,∴OE=ON=FN,∴t=![]() ×
×![]() (8﹣t),解得:t=
(8﹣t),解得:t=![]() ;
;
即在點M的運動過程中,能使得四邊形MNEF為正方形,t的值為![]() ;
;
(2)分兩種情況:
①當0<t≤2時,y=![]() ×
×![]() (8﹣t)×t=
(8﹣t)×t=![]() ,即
,即![]() (0<t≤2);
(0<t≤2);
②當2<t≤4時,如圖2所示:作GH⊥NF于H,由(1)得:NF=![]() (8﹣t),GH=NH,GH=2FH,∴GH=
(8﹣t),GH=NH,GH=2FH,∴GH=![]() NF=
NF=![]() (8﹣t),∴y=
(8﹣t),∴y=![]() NF′GH=
NF′GH=![]() ×
×![]() (8﹣t)×
(8﹣t)×![]() (8﹣t)=
(8﹣t)=![]() ,即
,即![]() (2<t≤4);
(2<t≤4);
綜上所述: .
.
(3)當點E在AB邊上時,y取最大值,連接EM,如圖3所示:
則EF=BF,EM=2CN=2CM=2t,EM=2BM,∵BM=4﹣t,∴2t=2(4﹣t),解得:t=2,∴CN=CM=2,AN=6,∴BM=4﹣2=2,NF=![]() AN=3,∴EM=2BM=4,作FD⊥NE于D,則EB=
AN=3,∴EM=2BM=4,作FD⊥NE于D,則EB=![]() =
=![]() =
=![]() ,△DNF是等腰直角三角形,∴EF=
,△DNF是等腰直角三角形,∴EF=![]() EB=
EB=![]() ,DF=
,DF=![]() HF=
HF=![]() ,在Rt△DEF中,sin∠NEF=
,在Rt△DEF中,sin∠NEF=![]() =
=![]() =
=![]() .
.


科目:初中數學 來源: 題型:
【題目】據統計,甘肅省定西市2018年全市常住人口280.84萬人,將數據280.84萬用科學記數法表為( )
A. 2.8084×102B. 2.8084×104C. 2.8084×106D. 2.8084×108
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】點A(3,y1,),B(-2,y2)都在直線y=-2x+3上,則y1與y2的大小關系是( )
A. y1>y2 B. y2>y1 C. y1=y2 D. 不能確定
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】江南農場收割小麥,已知1臺大型收割機和3臺小型收割機1小時可以收割小麥1.4公頃,2臺大型收割機和5臺小型收割機1小時可以收割小麥2.5公頃.
(1)每臺大型收割機和每臺小型收割機1小時收割小麥各多少公頃?
(2)大型收割機每小時費用為300元,小型收割機每小時費用為200元,兩種型號的收割機一共有10臺,要求2小時完成8公頃小麥的收割任務,且總費用不超過5400元,有幾種方案?請指出費用最低的一種方案,并求出相應的費用.
查看答案和解析>>
科目:初中數學 來源: 題型:
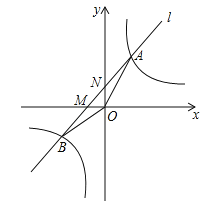
【題目】如圖,設反比例函數的解析式為![]() (k>0).
(k>0).
(1)若該反比例函數與正比例函數y=2x的圖象有一個交點的縱坐標為2,求k的值;
(2)若該反比例函數與過點M(﹣2,0)的直線l:y=kx+b的圖象交于A,B兩點,如圖所示,當△ABO的面積為![]() 時,求直線l的解析式.
時,求直線l的解析式.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】小明從家到圖書館看報然后返回,他離家的距離y與離家的時間x之間的對應關系如圖所示,如果小明在圖書館看報30分鐘,那么他離家50分鐘時離家的距離為 km.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某校為了豐富學生的校園生活,準備購進一批籃球和足球.其中籃球的單價比足球的單價多40元,用1500元購進的籃球個數與900元購進的足球個數相等.
(1)籃球和足球的單價各是多少元?
(2)該校打算用1000元購買籃球和足球,問恰好用完1000元,并且籃球、足球都買有的購買方案有哪幾種?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com