
(1)觀察與發現:將矩形紙片AOCB折疊,使點C與點A重合,點B落在點B′處(如圖),折痕為EF.小明發現△AEF為等腰三角形,你同意嗎?請說明理由.
(2)實踐與應用:以點O為坐標原點,分別以矩形的邊OC、OA為x軸、y軸建立如圖所示的直角坐標系,若頂點B的坐標為(9,3),請求出折痕EF的長及EF所在直線的函數關系式.
(1)同意,理由見解析;(2) ,y=3x-12.
,y=3x-12.
解析試題分析:(1)同意.
理由:因為AB∥OC,所以∠AEF=∠EFC.根據折疊性質,有∠AFE=∠EFC.所以∠AEF=∠AFE,AE=AF.△AEF為等腰三角形.
(2)過點E作EG⊥OC于點G.設OF=x,則CF=9-x;由折疊可知:AF=9-x.
在Rt△AOF中,AF2=AO2+OF2即:32+x2=(9-x)2,解得x=4,AE=AF=9-x=5,FG=OG-OF=5-4=1.在Rt△EFG中,EF2=EG2+FG2=10,求出EF=
設直線EF的解析式為y=kx+b(k≠0),因為點E(5,3)和點F(4,0)在直線EF上,所以,代入解得解得k,b,進而求出解析式.
試題解析:(1)同意.
理由:∵AB∥OC,∴∠AEF=∠EFC.
根據折疊性質,有∠AFE=∠EFC.
∴∠AEF=∠AFE,
∴AE=AF.
∴△AEF為等腰三角形.
(2)過點E作EG⊥OC于點G.
設OF=x,則CF=9-x;
由折疊可知:AF=9-x.
在Rt△AOF中,AF2=AO2+OF2
∴32+x2=(9-x)2,
∴x=4,9-x=5.
∴AE=AF=5,
∴FG=OG-OF=5-4=1.
在Rt△EFG中,
EF2=EG2+FG2=10,
∴EF=
設直線EF的解析式為y=kx+b(k≠0),
∵點E(5,3)和點F(4,0)在直線EF上,
∴3=5k+b,0=4k+b,
解得:k=3,b=-12.
∴y=3x-12.
考點:1.折疊問題.2.一次函數的解析式.3.勾股定理.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:初中數學 來源: 題型:解答題
某文具店準備購進甲,乙兩種鋼筆,若購進甲種鋼筆100支,乙種鋼筆50支,需要1000元,若購進甲種鋼筆50支,乙種鋼筆30支,需要550元.
(1)求購進甲,乙兩種鋼筆每支各需多少元?
(2)若該文具店準備拿出1000元全部用來購進這兩種鋼筆,考慮顧客需求,要求購進甲中鋼筆的數量不少于乙種鋼筆數量的6倍,且不超過乙種鋼筆數量的8倍,那么該文具店共有幾種進貨方案?
(3)若該文具店銷售每支甲種鋼筆可獲利潤2元,銷售每支乙種鋼筆可獲利潤3元,在第(2)問的各種進貨方案中,哪一種方案獲利最大?最大利潤是多少元?
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
某工廠現有甲種原料360kg,乙種原料290kg,計劃用它們生產A、B兩種產品共50件,已知每生產一件A種產品,需要甲種原料9kg、乙種原料3kg,獲利700元,生產一件B種產品,需要甲種原料4kg、乙種原料10kg,可獲利1200元.
(1)利用這些原料,生產A、B兩種產品,有哪幾種不同的方案?
(2)設生產兩種產品總利潤為y(元),其中生產A中產品x(件),試寫出y與x之間的函數解析式.
(3)利用函數性質說明,采用(1)中哪種生產方案所獲總利潤最大?最大利潤是多少?
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
如圖,已知直線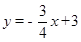 與x軸、y軸分別交于點A、B,線段AB為直角邊在第一象限內作等腰Rt△ABC,∠BAC=90°.
與x軸、y軸分別交于點A、B,線段AB為直角邊在第一象限內作等腰Rt△ABC,∠BAC=90°.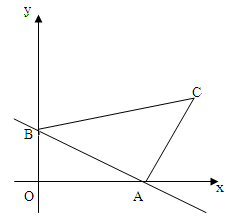
(1)求△AOB的面積;
(2)求點C坐標;
(3)點P是x軸上的一個動點,設P(x,0)
①請用x的代數式表示PB2、PC2;
②是否存在這樣的點P,使得|PC-PB|的值最大?如果不存在,請說明理由;
如果存在,請求出點P的坐標.
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
一次函數y=kx+4的圖象經過點(-3,-2),則
(1)求這個函數表達式;并畫出該函數的圖象.
(2)判斷(-5,3)是否在此函數的圖象上;
(3)求把這條直線沿x軸向右平移1個單位長度后的函數表達式.
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
國家推行“節能減排,低碳經濟”的政策后,某企業推出一種叫“CNG”的改燒汽油為天然氣的裝置,每輛車改裝費為b元.據市場調查知:每輛車改裝前、后的燃料費(含改裝費) 、
、 (單位:元)與正常運營時間
(單位:元)與正常運營時間 (單位:天)之間分別滿足關系式:
(單位:天)之間分別滿足關系式: 、
、 ,如圖所示.
,如圖所示.
試根據圖像解決下列問題:
(1)每輛車改裝前每天的燃料費 = 元,每輛車的改裝費b= 元.正常運營 天后,就可以從節省燃料費中收回改裝成本.
= 元,每輛車的改裝費b= 元.正常運營 天后,就可以從節省燃料費中收回改裝成本.
(2)某出租汽車公司一次性改裝了100輛車,因而,正常運營多少天后共節省燃料費40萬元?
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
如圖,一次函數 與反比例函數
與反比例函數 的圖象相交于點A,且點A的縱坐標為1.
的圖象相交于點A,且點A的縱坐標為1.
(1)求反比例函數的解析式;
(2)根據圖象寫出當x>0時,一次函數的值大于反比例函數的值的x的取值范圍.
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
閱讀材料:若a,b都是非負實數,則 .當且僅當a=b時,“=”成立.
.當且僅當a=b時,“=”成立.
證明:∵ ,∴
,∴ .
.
∴ .當且僅當a=b時,“=”成立.
.當且僅當a=b時,“=”成立.
舉例應用:已知x>0,求函數 的最小值.
的最小值.
解: .當且僅當
.當且僅當 ,即x=1時,“=”成立.
,即x=1時,“=”成立.
當x=1時,函數取得最小值,y最小=4.
問題解決:汽車的經濟時速是指汽車最省油的行駛速度.某種汽車在每小時70~110公里之間行駛時(含70公里和110公里),每公里耗油 升.若該汽車以每小時x公里的速度勻速行駛,1小時的耗油量為y升.
升.若該汽車以每小時x公里的速度勻速行駛,1小時的耗油量為y升.
(1)求y關于x的函數關系式(寫出自變量x的取值范圍);
(2)求該汽車的經濟時速及經濟時速的百公里耗油量(結果保留小數點后一位).
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
為了落實黨中央提出的“惠民政策”,我市今年計劃開發建設A、B兩種戶型的“廉租房”共40套.投入資金不超過200萬元,又不低于198萬元.開發建設辦公室預算:一套A型“廉租房”的造價為5.2萬元,一套B型“廉租房”的造價為4.8萬元.
(1)請問有幾種開發建設方案?
(2)哪種建設方案投入資金最少?最少資金是多少萬元?
(3)在(2)的方案下,為了讓更多的人享受到“惠民”政策,開發建設辦公室決定通過縮小“廉租房”的面積來降低造價、節省資金.每套A戶型“廉租房”的造價降低0.7萬元,每套B戶型“廉租房”的造價降低0.3萬元,將節省下來的資金全部用于再次開發建設縮小面積后的“廉租房”,如果同時建設A、B兩種戶型,請你直接寫出再次開發建設的方案.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com