【題目】某商店從廠家以21元的價格購進一批商品，該商品可以自行定價，若每件商品售價為
元，則可賣出（350－10）件，但物價局限定每件商品加價不能超過進價的20%，商店計劃要賺400元，需要賣出多少件商品?每件商品應售多少元？
科目：初中數學 來源： 題型：
【題目】如圖，直線BC//OA,∠C=∠OAB=100°,E，F在CB上，且滿足∠FOB=∠AOB,OE平分∠COF.
(1)求∠BOE的度數；
(2)若平行移動AB,那么∠OBC:∠OFC的值是否隨之發生變化?若變化,找出變化規律或求出變化范圍；若不變，求出這個比值（提示:圖中∠OFC=∠BOF+∠OBC）；
(3)在平行移動AB的過程中,是否存在某種情況,使∠OEC=∠OBA?若存在,求出∠OEC度數；若不存在,說明理由(提示：三角形三個內角的和為180）.
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】中國人很早就開始使用負數，中國古代數學著作《九章算術》．如果收入120元記作+120元，那么-100元表示( )
A.支出20元B.支出100元C.收入20元D.收入100元
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】學校想知道九年級學生對我國倡導的“一帶一路”的了解程度，隨機抽取部分九年級學生進行問卷調查，問卷設有4個選項（每位被調查的學生必選且只選一項）：A．非常了解．B．了解．C．知道一點．D．完全不知道．將調查的結果繪制如下兩幅不完整的統計圖，請根據兩幅統計圖中的信息，解答下列問題：
（1）求本次共調查了多少學生？
（2）補全條形統計圖；
（3）該校九年級共有600名學生，請你估計“了解”的學生約有多少名？
（4）在“非常了解”的3人中，有2名女生，1名男生，老師想從這3人中任選兩人做宣傳員，請用列表或畫樹狀圖法求出被選中的兩人恰好是一男生一女生的概率．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖①，△ABC中，∠ABC與∠ACB的平分線交于點I.根據下列條件，求∠BIC的
度數。
（1）若∠ABC=60°，∠ACB=70°,則∠BIC=
（2）若∠ABC+∠ACB=130°，則∠BIC=
（3）若∠A=50°，則∠BIC=
（4）若∠A=110°，則∠BIC=
（5）從上述計算中，我們能發現已知∠A，求∠BIC的公式是：∠BIC= .
（6）如圖②，BP，CP分別是∠ABC與∠ACB的外角平分線，交于點P.
若已知∠A，則求∠BPC的公式是：∠BPC=
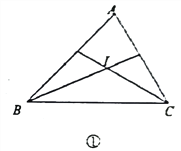
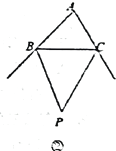
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，已知點D、F、E、G都在△ABC的邊上，EF∥AD，∠1=∠2，∠BAC=70°，求∠AGD的度數．（請在下面的空格處填寫理由或數學式）
解：∵EF∥AD，（已知）
∴∠2= （ ）
∵∠1=∠2，（已知）
∴∠1= （ ）
∴ ∥ ，（ ）
∴∠AGD+ =180°，（兩直線平行，同旁內角互補）
∵ ，（已知）
∴∠AGD= （等式性質）
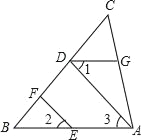
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】已知直線
，直線
與直線
、
分別相交于C、D兩點．
（1）如圖a，有一動點P在線段CD之間運動(不與C、D兩點重合)，問在點P的運動過程中，是否始終具有∠3+∠1=∠2這一關系，為什么？
（2）如圖b，當動點P線段CD之外運動(不與C、D兩點重合)，問上述結論是否成立?若不成立，試寫出新的結論并說明理由．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】（1）閱讀理解：如圖①，在四邊形ABCD中，AB∥DC，E是BC的中點，若AE是∠BAD的平分線，試判斷AB，AD，DC之間的等量關系．
解決此問題可以用如下方法：延長AE交DC的延長線于點F，易證△AEB≌△FEC，得到AB=FC，從而把AB，AD，DC轉化在一個三角形中即可判斷．
AB、AD、DC之間的等量關系為 ；
（2）問題探究：如圖②，在四邊形ABCD中，AB∥DC，AF與DC的延長線交于點F，E是BC的中點，若AE是∠BAF的平分線，試探究AB，AF，CF之間的等量關系，并證明你的結論．
（3）問題解決：如圖③，AB∥CF，AE與BC交于點E，BE：EC=2：3，點D在線段AE上，且∠EDF=∠BAE，試判斷AB、DF、CF之間的數量關系，并證明你的結論．
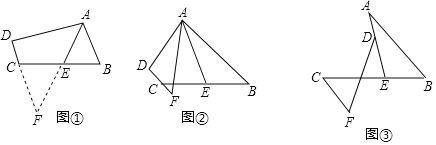
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
