
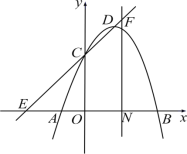
【題目】已知拋物線y=-x2+2x+3與x軸交于A、B兩點(點A在點B的左側),與y軸交于點C,頂點為D,直線CD與x軸交于點E.
(1)求A、B的坐標;
(2)求點E的坐標;
(3)過線段OB的中點N作x軸的垂線并交直線CD于點F,則直線NF上是否存在點M,使得點M到直線CD的距離等于點M到原點O的距離?若存在,求出點M的坐標;若不存在,請說明理由.
【答案】(1)點A的坐標(-1,0),點B的坐標(3,0);(2)(-3,0);(3)存在,(![]() ,
,![]() )或(
)或(![]() ,
,![]() )
)
【解析】
(1)拋物線y=-x2+2x+3與x軸兩個交點的橫坐標即是方程-x2+2x+3=0的兩個實數根;
(2)先根據二次函數表達式算出點C與頂點D,再用待定系數法算出直線CD的解析式,最后算出點E坐標即可;
(3)存在滿足條件的點M(![]() ,m),過點M作MQ⊥CD于Q,連接OM,先證明Rt△FQM∽Rt△FNE,再利用相似的性質得到關于m的方程,解方程即可.
,m),過點M作MQ⊥CD于Q,連接OM,先證明Rt△FQM∽Rt△FNE,再利用相似的性質得到關于m的方程,解方程即可.
解:(1)由y=0得-x2+2x+3=0,
解得x1=-1,x2=3,
∴點A的坐標(-1,0),點B的坐標(3,0)
(2)由y=-x2+2x+3,令x=0,得y=3,
∴C(0,3)
又∵y=-x2+2x+3=-(x-1)2+4,
得D(1,4)
設直線CD的解析式為y=kx+b,得
![]() ,
,
解得:![]() ,
,
∴直線CD的解析式為y=x+3
∴E(-3,0)
(3)存在.
由(1)(2)得,E(-3,0),N(![]() ,0)
,0)
∴F(![]() ,
, ![]() ),EN=
),EN=![]() ,
,
設存在滿足條件的點M(![]() ,m),作MQ⊥CD于Q,則
,m),作MQ⊥CD于Q,則
FM=![]() , EF=
, EF=![]() , MQ=OM=
, MQ=OM=![]()
由題意得:Rt△FQM∽Rt△FNE,
∴![]() ,
,
∴4m2
∴m1= ![]() ,m2=
,m2=![]() ,
,
∴點M的坐標為M1(![]() ,
,![]() ),M2(
),M2(![]() ,
,![]() )
)



科目:初中數學 來源: 題型:
【題目】《九章算術》是我國古代數學的經典著作,書中有一個問題:“今有黃金九枚,白銀一十一枚,稱之重適等,交易其一,金輕十三兩,問金、銀各重幾何?”意思是:甲袋中裝有黃金9枚(每枚黃金重量相同),乙袋中裝有白銀11枚(每枚白銀重量相同),稱重兩袋相等,兩袋互相交換1枚后,甲袋比乙袋輕了13兩(袋子重量忽略不計),問黃金、白銀每枚各重多少兩?
查看答案和解析>>
科目:初中數學 來源: 題型:
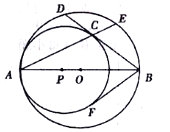
【題目】如圖,![]() 為⊙
為⊙![]() 的直徑,點
的直徑,點![]() 是半徑
是半徑![]() 上一個動點(不與點
上一個動點(不與點![]() 重合),
重合),![]() 為⊙
為⊙![]() 的半徑,⊙
的半徑,⊙![]() 的弦
的弦![]() 與⊙
與⊙![]() 相切于點
相切于點![]() ,
,![]() 的延長線交⊙
的延長線交⊙![]() 于點
于點![]() .
.
(1)設![]() ,則
,則![]() 與
與![]() 之間的數量關系是什么?請說明理由.
之間的數量關系是什么?請說明理由.
(2)若![]() ,點
,點![]() 關于
關于![]() 的對稱點為
的對稱點為![]() ,連接
,連接![]() .
.
①當![]() 時,四邊形
時,四邊形![]() 是菱形;
是菱形;
②當![]() 時,點
時,點![]() 是弦
是弦![]() 的中點.
的中點.
查看答案和解析>>
科目:初中數學 來源: 題型:
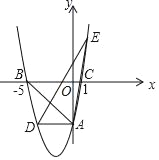
【題目】如圖,在平面直角坐標系中,拋物線y=ax2+bx﹣5交y軸于點A,交x軸于點B(﹣5,0)和點C(1,0),過點A作AD∥x軸交拋物線于點D.
(1)求此拋物線的表達式;
(2)點E是拋物線上一點,且點E關于x軸的對稱點在直線AD上,求△EAD的面積;
(3)若點P是直線AB下方的拋物線上一動點,當點P運動到某一位置時,△ABP的面積最大,求出此時點P的坐標和△ABP的最大面積.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】關于x的二次函數![]() (k為常數)和一次函數
(k為常數)和一次函數![]() .
.
(1)求證:函數![]() 的圖象與x軸有交點.
的圖象與x軸有交點.
(2)已知函數![]() 的圖象與x軸的兩個交點間的距離等于3,
的圖象與x軸的兩個交點間的距離等于3,
①試求此時k的值.
②若![]() ,試求x的取值范圍.
,試求x的取值范圍.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】星星和陽陽是一對雙胞胎,他們的爸爸買了兩件不同圖案的T恤給他們,星星和陽陽都想先挑選.于是陽陽設計了如下游戲來決定誰先挑選.游戲規則是:在一個不透明的袋子里裝有除數字以外其它均相同的![]() 個小球,上面分別標有數字
個小球,上面分別標有數字![]() .一人先從袋中隨機摸出一個小球,另一人再從袋中剩下的
.一人先從袋中隨機摸出一個小球,另一人再從袋中剩下的![]() 個小球中隨機摸出一個小球.若摸出的兩個小球上的數字之和為偶數,則星星先挑選;否則陽陽先挑選.
個小球中隨機摸出一個小球.若摸出的兩個小球上的數字之和為偶數,則星星先挑選;否則陽陽先挑選.
(1)用樹狀圖或列表法求出星星先挑選的概率;
(2)你認為這個游戲公平嗎?請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】隨著國內疫情基本得到控制,旅游業也慢慢復蘇,經市場調研發現旅游景點未來![]() 天內,旅游人數
天內,旅游人數![]() 與時間
與時間![]() 的關系如下表;每張門票
的關系如下表;每張門票![]() 與時間
與時間![]() 之間存在如下圖所示的一次函數關系.(
之間存在如下圖所示的一次函數關系.(![]() ,且
,且![]() 為整數)
為整數)
時間 |
|
|
|
|
|
人數 |
|
|
|
|
|
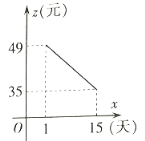
請結合上述信息解決下列問題:
(1)直接寫出:![]() 關于
關于![]() 的函數關系式是 .
的函數關系式是 .![]() 與時間
與時間![]() 函數關系式是 .
函數關系式是 .
(2)請預測未來![]() 天中哪一天的門票收入最多,最多是多少?
天中哪一天的門票收入最多,最多是多少?
(3)為支援武漢抗疫,該旅游景點決定從每天獲得的門票收入中拿出![]() 元捐贈給武漢紅十字會,求捐款后共有幾天每天剩余門票收入不低于
元捐贈給武漢紅十字會,求捐款后共有幾天每天剩余門票收入不低于![]() 元?
元?
查看答案和解析>>
科目:初中數學 來源: 題型:
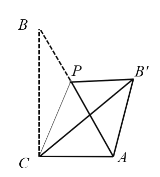
【題目】已知,Rt△ABC中,∠ACB=90°,∠B=30°,AC=1,點P是AB上一點,連接CP,將∠B沿CP折疊,使點B落在B'處.以下結論正確的有________
①當AB'⊥AC時,AB'的長為![]() ;
;
②當點P位于AB中點時,四邊形ACPB'為菱形;
③當∠B'PA=30°時,![]() ;
;
④當CP⊥AB時,AP:AB':BP=1:2:3.
查看答案和解析>>
科目:初中數學 來源: 題型:
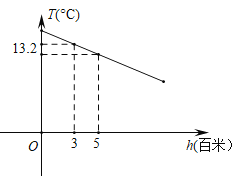
【題目】某地區山峰的高度每增加1百米,氣溫大約降低0.6℃.氣溫T(℃)和高度h(百米)的函數關系如圖所示.請根據圖象解決下列問題:
(1)求高度為5百米時的氣溫.
(2)求T關于h的函數表達式.
(3)測得山頂的氣溫為6℃,求該山峰的高度.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com