
【題目】如圖, ![]() 是等邊三角形,延長
是等邊三角形,延長![]() 到點
到點![]() ,延長
,延長![]() 到點
到點![]() ,使
,使![]() ,連接
,連接![]() ,延長
,延長![]() 交
交![]() 于
于![]() .
.
(1)求證: ![]() ;
;
(2)求![]() 的度數.
的度數.
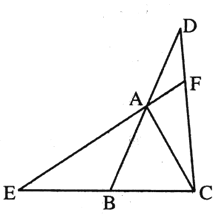
【答案】(1)證明見解析;(2)60°
【解析】
(1)根據等邊三角形的性質得到AB=AC,∠DAC=∠ABE=120°,結合![]() 可證明△ABE≌△ACD,可得∠BAE=∠ACD,AE=CD,故可得∠EAC=∠DCB,,進一步可證明
可證明△ABE≌△ACD,可得∠BAE=∠ACD,AE=CD,故可得∠EAC=∠DCB,,進一步可證明![]() ;
;
(2)根據全等三角形的性質得到∠E=∠D,∠ EAB=∠DAF,根據三角形的外角的性質得到結論.
(1)證明:∵△ABC是等邊三角形,
∴AB=AC,∠CAB=∠ABC=60°,
∴∠DAC=∠ABE=120°,
在△ABE和△ACD中,
 ,
,
∴△ABE≌△ACD,
∴AE=CD,∠BAE=∠ACD,
∴∠CAE=∠BCD,
在△ACE和△CBD中
 ,
,
∴![]() ;
;
(2)∵△ABE≌△ACD,
∴∠E=∠D,
∴∠CFE=∠D+∠DAF
=∠E+∠EAB,
=∠ABC,
=60°.


 超能學典應用題題卡系列答案
超能學典應用題題卡系列答案科目:初中數學 來源: 題型:
【題目】如圖,在邊長為5的正方形ABCD中,以A為一個頂點,另外兩個頂點在正方形ABCD的邊上,且含邊長為3的所有大小不同的等腰三角形的個數為( )

A.3B.4C.5D.6
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖所示,矩形ABCD中,AE平分![]() 交BC于E,
交BC于E,![]() ,則下面的結論:①
,則下面的結論:①![]() 是等邊三角形;②
是等邊三角形;②![]() ;③
;③![]() ;④
;④![]() ,其中正確結論有( )
,其中正確結論有( )
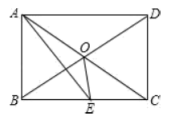
A. 1個B. 2個C. 3個D. 4個
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在△ABC中,E是AC邊上的一點,且AE=AB,∠BAC=2∠CBE,以AB為直徑作⊙O交AC于點D,交BE于點F.
(1)求證:BC是⊙O的切線;
(2)若AB=8,BC=6,求DE的長.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在平面直角坐標系中,矩形OABC的邊OA,OC分別位于x軸,y軸上,經過A,C兩點的拋物線變x軸于另一點D,連接AC.請你只用無刻度的直尺按要求畫圖.
(1)在圖1中的拋物線上,畫出點E,使DE=AC;
(2)在圖2中的拋物線上,畫出拋物線的頂點F.
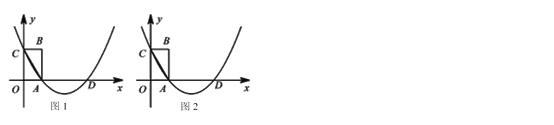
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某商場用3000元購進某種商品,由于銷售狀況良好,商場又用9000元購進這種商品,但這次的進價比第一次的進價提高了20%,購進商品比第一次的2倍還多300千克,如果商場按每千克9元出售.
求:(1)該種商品第一次的進價是每千克多少元?
(2)超市銷售完這種商品共盈利多少元?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖是小李上學用的自行車,型號是24英吋(車輪的直徑為24英吋,約60厘米),為了防止在下雨天騎車時的泥水濺到身上,他想在自行車兩輪的陰影部分兩側裝上擋水的鐵皮(兩個陰影部分分別是以C、D為圓心的兩個扇形),量出四邊形ABCD中∠DAB=125°、∠ABC=115°,那么預計需要的鐵皮面積約是( )

A. 942平方厘米 B. 1884平方厘米
C. 3768平方厘米 D. 4000平方厘米
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在△ABC中,∠ABC=60°,AC=2AB,AD平分∠BAC交BC于點D,延長DB至點F,使BF=BD連接AF.
(1)求證:AF=CD.
(2)若CE平分∠ACB交AB于點E,試猜想AC,AF,AE三條線段之間的數量關系,并證明你的猜想.

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com