
【題目】如圖,P是正三角形ABC內的一點,且PA=6,PB=8,PC=10.若將△PAC繞點A逆時針旋轉后,得到△P′AB.
(1)求點P與點P′之間的距離;
(2)求∠APB的度數.

【答案】(1)6;(2)150°.
【解析】
(1)連結PP′,由旋轉性質可知BP′=PC=10,AP′=AP,∠PAC=∠P′AB,根據∠PAC+∠BAP=∠P′AB+∠BAP=60°可得△APP′為等邊三角形,即可證明PP′=AP=6;(2)利用勾股定理的逆定理可得△BPP′為直角三角形,且∠BPP′=90°,由(1)得∠APP′=60°,即可得答案.
(1)連接PP′,由題意可知BP′=PC=10,AP′=AP,∠PAC=∠P′AB,
∵∠PAC+∠BAP=∠BAC=60°,
∴∠PAP′=∠P′AB+∠BAP=∠PAC+∠BAP=60°.
∴△APP′為等邊三角形,
所以PP′=AP=AP′=6;
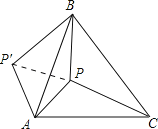
(2)∵PP′=6,BP=8,BP′=10,
∴PP′2+BP2=BP′2,
∴△BPP′為直角三角形,且∠BPP′=90°
∴∠APB=∠BPP′+∠APP′=90°+60°=150°.


科目:初中數學 來源: 題型:
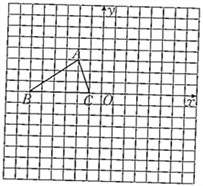
【題目】如圖,已知△ABC的三個頂點的坐標分別為A(-2,3)、B(-6,0)、C(-1,0).
(1)畫出將△ABC繞坐標原點O逆時針旋轉90°圖形.
(2)填空:以A、B、C為頂點的平行四邊形的第四個頂點D的坐標為________.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,△ABC面積為1,第一次操作:分別延長AB,BC,CA至點A1,B1,C1,使A1B=AB,B1C=BC,C1A=CA,順次連接A1,B1,C1,得到△A1B1C1.第二次操作:分別延長A1B1,B1C1,C1A1至點A2,B2,C2,使A2B1=A1B1,B2C1=B1C1,C2A1=C1A1,順次連接A2,B2,C2,得到△A2B2C2,…按此規律,第n次操作后,得到△AnBnCn,要使△AnBnCn的面積超過2020,則至少需要操作__________次.

查看答案和解析>>
科目:初中數學 來源: 題型:
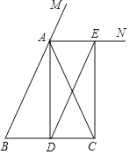
【題目】已知:如圖,在△ABC中,AB=AC,AD是△ABC的中線,AN為△ABC的外角∠CAM的平分線,CE∥AD,交AN于點E.求證:四邊形ADCE是矩形.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知△ABC中,AB=AC,∠BAC=90°,直角∠EPF的頂點P是BC中點,兩邊PE、PF分別交AB、AC于點E、F,當∠EPF在△ABC內繞頂點P旋轉時(點E不與A、B重合),給出以下四個結論:①AE=CF;②△EPF是等腰直角三角形;③2S四邊形AEPF=S△ABC;④BE+CF=EF.上述結論中始終正確的有( )

A. 4個 B. 3個 C. 2個 D. 1個
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】新定義:我們把只有一組對角是直角的四邊形叫做準矩形.
(1)圖①、圖②均為3×3的正方形網格,每個小正方形的頂點稱為格點,每個小正方形的邊長均為1.線段AB、BC的端點均在格點上,在圖①、圖②中各畫一個準矩形ABCD,要求:準矩形ABCD的頂點D在格點上,且兩個準矩形不全等.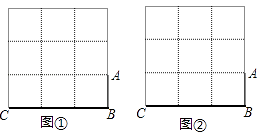
(2)如圖③,正方形ABCD的邊長為4,準矩形ABMN的頂點M、N分別在正方形ABCD的邊上.若準矩形ABMN的一條對角線長為5,直接寫出此時該準矩形的面積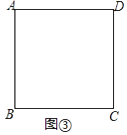
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】從甲、乙兩名射擊選手中選出一名選手參加省級比賽,現對他們分別進行5次射擊測試,成績分別為(單位:環)甲:5、6、7、9、8;乙:8、4、8、6、9,
(1)甲運動員5次射擊成績的中位數為________環,極差是________環;乙運動員射擊成績的眾數為________環.
(2)已知甲的5次成績的方差為2,通過計算,判斷甲、乙兩名運動員誰的成績更穩定.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com