在一個不透明的盒子里裝有5個分別寫有數(shù)字-2,-1,0,1,2的小球,它們除數(shù)字不同外其余全部相同.現(xiàn)從盒子里隨機取出一個小球,將該小球上的數(shù)字作為點P的橫坐標,將該數(shù)的平方作為點P的縱坐標,則點P落在拋物線y=-x2+2x+5與x軸所圍成的區(qū)域內(不含邊界)的概率是 .
【答案】
分析:畫出拋物線圖象,確定各點橫坐標所對應的縱坐標,與P點縱坐標比較即可.
解答: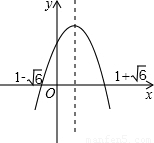
解:如圖,
-2,-1,0,1,2的平方為4,1,0,1,4.
點P的坐標為(-2,4),(-1,1),(0,0),(1,1),(2,4);
描出各點:-2<1-
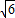
,不合題意;
把x=-1代入解析式得:y
1=2,1<2,故(-1,1)在該區(qū)域內;
把x=0代入解析式得:y
2=5,0<5,故(0,0)在邊界上,不在區(qū)域內;
把x=1代入解析式得:y
3=6,1<6,故(1,1)在該區(qū)域內;
把x=2代入解析式得:y
4=5,4<5,故(2,4)在該區(qū)域內.
所以5個點中有3個符合題意,
點P落在拋物線y=-x
2+2x+5與x軸所圍成的區(qū)域內(不含邊界)的概率是

.
點評:本題考查了概率的簡單計算能力,是一道列舉法求概率的問題,屬于基礎題,可以直接應用求概率的公式:P(A)=
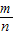
.

 解:如圖,
解:如圖,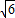 ,不合題意;
,不合題意; .
.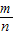 .
. 
