
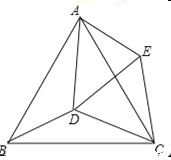
【題目】如圖,已知等邊△ABC,點D為△ABC內一點,連接DA、DB、DC,∠ADB=120°.以CD為邊向CD上方作等邊△CDE,連接AE.(0°<∠ACE<60°)
(1)求證:△BDC≌△AEC;
(2)若DA=![]() +1,DB=
+1,DB=![]() ﹣1,DC=2n(n為大于1的整數),求∠BDC的度數;
﹣1,DC=2n(n為大于1的整數),求∠BDC的度數;
(3)若△ADE為等腰三角形,求![]() 的值.
的值.
【答案】(1)證明詳見解析;(2)150°;(3)![]() .
.
【解析】
試題分析:(1)由等邊三角形的性質得出結論,直接用SAS得出結論;
(2)用等邊三角形的性質得出DE=CD,進而判斷出△ADE是直角三角形,即可得出結論;
(3)分三種情況先判斷出△ADE是等邊三角形,進而構造出直角三角形,用含30°的直角三角形的性質得出結論即可.
試題解析:(1)∵△ABC和△CDE是等邊三角形,
∴BC=AC,CD=CE=DE,∠ACB=∠DCE=∠CED=60°,
∴∠BCD=∠ACE,
在△BDC和△AEC中,
BC=AC,∠BCD=∠ACE,CE=CE,
∴△BDC≌△AEC(SAS);
(2)由(1)知,DE=CD=2n,△BDC≌△AEC,
∴∠BDC=∠AEC,AE=BD=![]() ﹣1,
﹣1,
∵DA=![]() +1,AE=
+1,AE=![]() ﹣1,DE=2n,
﹣1,DE=2n,
∴![]() =
=![]() =
=![]() ,
,
∴△ADE是直角三角形,
∴∠AED=90°,
∴∠BDC=∠AEC=∠AED+∠CED=150°;
(3)如圖,
①當AD=AE時,由(1)知,△BDC≌△AEC,
∴∠CAE=∠CBD,AE=BD,
∴AD=BD,
∵∠ADB=120°,
∴∠BAD=∠ABD=30°,
∵∠ABC=∠BAC=60°,
∴∠CBD=∠CAD=∠CAE=30°,
∴∠DAE=60°,
∴△ADE是等邊三角形;
②當AD=DE時,∵CD=DE,
∴AD=CD,
∴∠CAD=∠DCA,
∵∠BAC=∠BCA,
∴∠BAD=∠BCD,
在△ABD和△CBD中,
AB=BC,∠BAD=∠BCD,AD=CD,
∴△ABD≌△CBD,
∴∠ABD=![]() ∠ABC=30°,
∠ABC=30°,
以后同①的方法得出,△ADE是等邊三角形,
③當AE=DE時,同②的方法得出,△ADE是等邊三角形,
即:△ADE是等邊三角形
過點D作DF⊥BC,
∴BC=2CF,在Rt△CDF中,∠DCF=30°,
∴cos30°=![]() ,
,
∴![]() =
=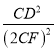 =
=![]() .
.


科目:初中數學 來源: 題型:
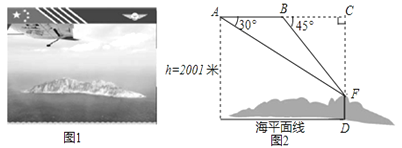
【題目】國家海洋局將中國釣魚島最高峰命名為“高華峰”,并對釣魚島進行常態化立體巡航.如圖1,在一次巡航過程中,巡航飛機飛行高度為2001米,在點A測得高華峰峰頂F點的俯角為30°,保持方向不變前進1200米到達B點后測得峰頂F點俯角為45°,如圖2.請據此計算釣魚島的最高海拔高度是多少米.(結果保留整數,參考數值:![]() =1.732,
=1.732,![]() =1.414)
=1.414)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】下列是假命題的是( )
A.兩點之間,線段最短
B.過一點有且只有一條直線與已知直線垂直
C.直角三角形的兩個銳角互余
D.兩條直線被第三條直線所截,同位角相等
查看答案和解析>>
科目:初中數學 來源: 題型:
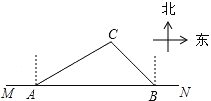
【題目】2009年3月21日邵陽市榮獲“省衛生城市稱號”,在創衛過程中,要在東西方向M、N兩地之間修建一條道路,已知:如圖,C點周圍180米范圍內為文物保護區,在MN上點A處測得C在A的北偏東60°方向上,從A向東走500米到達B處,測得C在B的北偏西45°方向上,問MN是否穿過文物保護區?為什么?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com